Оглавление:



Понятие о неразрезных балках и особенности их расчета
- Понятие непрерывных балок Особенности его расчета В практике строительства часто встречаются статические неопределенные балки, которые перекрывают несколько пролетов. Такие лучи называются непрерывными. Крайняя опора этих балок может быть
шарнирной или герметичной, а промежуточная опора-шарнирно подвижной. Если крайняя опора шарнирно закреплена, то одна из опор должна быть шарнирно закреплена для обеспечения геометрической инвариантности системы. Рис 283D
Чем больше промежуточная опора непрерывной балки, тем сложнее будет ее Людмила Фирмаль
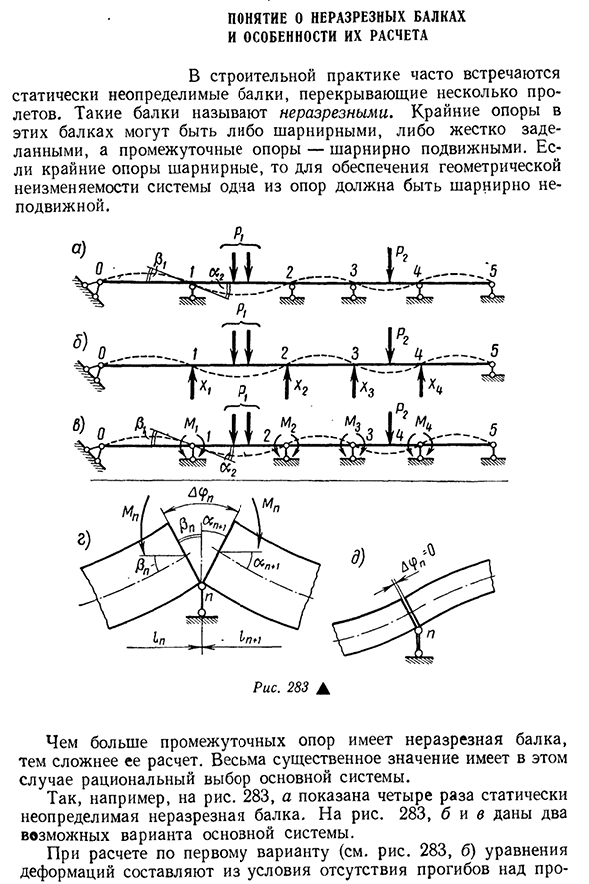
расчет. В этом случае очень важен рациональный выбор базовой системы. Например, на рисунке. 283, и показывают четыре раза статический неопределенный непрерывный свет. Для риса. 283, b и C являются двумя возможными вариантами базовой системы. При
расчете по первому варианту (см. фиг. 283, б) уравнение деформации состоит из состояния, в котором отсутствует прогиб про — И приказ № 1037 321 с ежедневной поддержкой. Итак, опору 1 можно записать как=a1R»B a1X1+y1x2y\x4=O» (Yu-9), где p p-1 основной системы, вызванной нагрузкой P Мы строим аналогичное уравнение для
- остальных трех опор и получаем четыре уравнения с четырьмя неизвестными. Во втором варианте основной системы (см. схему. 283, с)непрерывная балка преобразуется в четыре простых двухопорных балки путем размещения полного шарнира над промежуточной опорой. В этом случае изгибающий момент на промежуточной опоре является дополнительным неизвестным. Величина момента M1 (M2, M3) определяется из условия неразрывности балки на опоре.
Например, на правой стороне опоры касательные к упругой кривой должны совпадать как в точках до, так и после введения шарнира(1=A2, фиг. 283, а и Б). Для риса. 283, g указывает на поддержку p в основной системе. После установки шарнира поверх опоры Р-образного пролета, лежащего слева и справа от опоры, он деформируется внешними нагрузками независимо друг от друга. Раздел выше поддержки, принадлежащих к левому изменения распространяются на угол РЛ,а также раздел принадлежащих на праве изменений, охватывающие угол Ал+1. «
Раскрытие поперечного сечения» на углах DFLL происходит таким же образом. Из условий Людмила Фирмаль
непрерывности упругой кривой в сплошной балке этот угол равен нулю(рис. 283,5). Таким образом, уравнение деформации N-й опоры записывается в виде=RL+a l+1=0-углы RL и al+1 зависят от внешней нагрузки и неизвестных моментов M n^, M n и ml+1. В вариантах обоих возможных решений получается система одновременных уравнений, число которых равно степени статической неопределенности пучка. В первом варианте следует отметить, что система уравнений является полной, то есть каждая из n формул содержит n неизвестных. Эта ситуация объясняется тем, что из неизвестного все точки, в которых применяются X2, X3, X±, движутся через основную систему. Во втором варианте система уравнений
будет неполной. Каждое уравнение входит независимо от степени статической некоторые- Система имеет не более трех неизвестных, так как деформации, возникающие из любого из неизвестных, распространяются только в пределах двух соседних пролетов. Поэтому второе решение гораздо проще, особенно для систем с большим количеством неизвестных. Уравнения деформации для второй деформации основной системы называется уравнением трех моментов. Эта проблема подробно изучается в курсе «статическая структура».
Смотрите также:

