Оглавление:



Понятие о напряжениях и деформациях в точке
- Концепция стресса и деформации В то время Исходя из предыдущих предположений о непрерывности тела, можно предположить, что внутренние силы непрерывно распределяются по поперечному
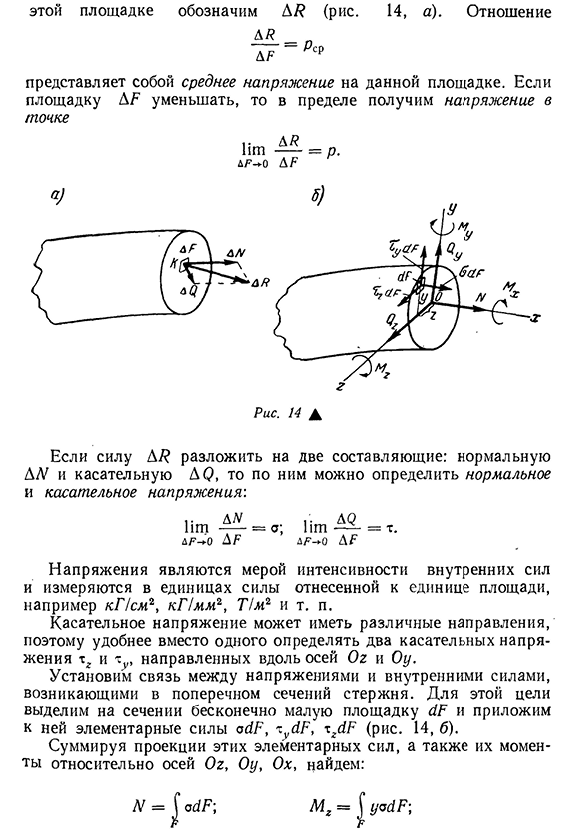
сечению. Выберите небольшую область AF в любой точке K, <6 А /? (Рисунок 14, а). отношение A /? & F Рк Представляет среднее напряжение на конкретном сайте
. Когда зона АФ уменьшается, Людмила Фирмаль
напряжение приобретается в пределах предела. Рис. 14 К Force A /? Если вы разложите на два компонента, нормальный A2V и касательный AQ, вы сможете определить нормальные и касательные напряжения по ним. Напряжение является мерой силы внутренних сил, единиц силы на единицу площади, например, кг / см2, кг!
Измеряется в Мм2, Т / м2 и т. Д. Поскольку напряжение сдвига может принимать разные направления, более удобно определять два касательных напряжения tg и xy, а не одно, ориентированное вдоль осей Oz и Oy. Установите связь между напряжением, создаваемым в поперечном сечении стержня, и внутренней силой. Для этого
- выбирается небольшая площадь dF на поперечном сечении и к ней применяются основные силы adF, xy dF, xzdF (рис. 14, б). Суммируя эти основные силовые проекции и моменты вокруг осей Oz, Oy, Oh, мы можем увидеть: N = J adF; Mg = §yodF \ F Символ F для интегрирования 17 указывает, что интегрирование выполняется по всей площади поперечного сечения. Используя приведенную выше формулу, вы можете определить результирующую силу внутренней силы из-за
напряжения, если вы знаете закон распределения для поперечного сечения. Невозможно решить обратную задачу, используя только показанные уравнения, потому что разные законы распределения нормальных напряжений по поперечному сечению могут соответствовать одному и тому же значению внутренней силы, например Af Пожалуйста, будьте осторожны. Одной из основных задач сопротивления материала является проблема определения напряжения, возникающего в результате внутренних сил.
Видно, что эту проблему можно решить только путем параллельного Людмила Фирмаль
рассмотрения состояний равновесия и деформации пучка. Чтобы определить деформацию в точке / C, рассмотрим небольшой сегмент, который начинается в любом направлении от этой точки (рис. 15). В результате преобразования точка K является точкой / <! И сегмент s становится длиннее на As и меняет направление. Ограничения отношений Называется относительной линейной деформацией в точке / C в направлении s. Если вы нарисуете три оси в точке K, параллельной координатным осям Ox, Oy, Og, линейные деформации в направлениях этих осей будут rx, ey и, например, соответственно. Из-за деформации, во-первых, прямой угол между минутными отрезками dx, dy, dz, исходящими из точки K, меняется на малые углы ixv, yy, Tug. Эти перпендикулярные изменения являются точками / (. D L A B A II, где присутствуют три линейные и три угловые составляющие деформации Растянуть и
Смотрите также:
| Преобразование моментов инерции при повороте осей | Продольные силы и их эпюры |
| Главные оси и главные моменты инерции | Напряжения и деформации при растяжении и сжатии |

