Понятие о функциональной, статистической и корреляционной зависимостях
Поведение и значение любого экономического показателя зависит от множества факторов, хотя только их ограниченное количество существенно воздействует на исследуемый экономический показатель. Выделение и учет в модели лишь ограниченного числа факторов оказывающих существенное влияние на развитие моделируемого экономического процесса, определение их взаимосвязи, являются ключевыми для принятия решений.
Остановимся вначале на изучении взаимосвязей между двумя переменным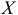и 
и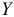 
, составляющими двумерной случайной величины 
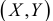. Если каждому значению одной случайной величины по некоторому
правилу относится одно значение другой случайной величины, то говорят о функциональной зависимости. В подавляющем большинстве случаев между экономическими переменными таких зависимостей нет. Это связано с целым рядом причин, поскольку при анализе влияния одной переменной на другую не учитывается ряд других факторов, влияющих на нее, и это влияние может быть не прямым, а косвенным и, кроме того, это влияние может носить случайный характер.
Зависимость между случайными величинами, имеющими общие случайные факторы, которые влияют как на одну, так и на другую случайную величину наряду с другими неодинаковыми для обеих случайных величин факторами, называется стохастической (вероятностной).
Так как при построении эконометрических моделей используются значения случайных величин (эмпирические значения), то стохастическую зависимость называют статистической.
Зависимость между исследуемыми случайными величинами называется статистической, если каждому эмпирическому значению одной случайной величины (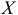) соответствует условное распределение эмпирических данных другой случайной величины ().
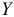На практике при обработке эмпирических данных
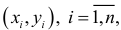
двумерной случайной величины 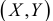находят оценку регрессионной связи, т.е. оценку функции регрессии
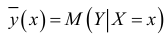
или
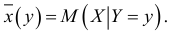
Для этого используются эмпирические функции регрессии, содержащие случайную составляющую:
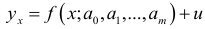
или
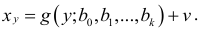
Таким образом, регрессия — это односторонняя стохастическая зависимость между значениями одной случайной величины и условными математическими значениями другой случайной величины. Случайная составляющая подчеркивает факт не совпадения реальных значений с условными математическими ожиданиями этих значений.
В зависимости от числа случайных величин, описывающих изучаемый экономический процесс, различают простую регрессию и множественную. Простая регрессия может быть положительной или отрицательной. При положительной регрессии с увеличением (уменьшением) независимой случайной величины увеличивается (уменьшается) зависимая случайная величина. При отрицательной регрессии — при увеличении (уменьшении) независимой случайной величины уменьшается (увеличивается) зависимая случайная величина.
По форме различают линейную регрессию и нелинейную, т.е. регрессию, выражаемую линейной и нелинейной функциями. В зависимости от типа соответствия между случайными величинами рассматривают непосредственную регрессию и косвенную. При непосредственной регрессии случайные величины связаны непосредственно друг с другом; при косвенной регрессии они детерминируются общей для них причиной.
Понятие регрессии тесно переплетается с понятием корреляции. Если в регрессионном анализе исследуется форма стохастической связи, то в корреляционном анализе оценивается интенсивность этой связи. Оба вида анализа служат для установления причинных соотношений между признаками изучаемых явлений и определения наличия или отсутствия связи между ними.
В зависимости от числа переменных величин, корреляция, может быть, простой (парной), или множественной. Корреляция между двумя случайными величинами называется простой, а между более чем двумя переменными — множественной. Корреляция между двумя переменными при фиксированном значении остальных переменных для случая множественной корреляции называется частной. Простая корреляция может быть положительной или отрицательной. Корреляция может быть линейной или нелинейной; непосредственной или косвенной.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
