Оглавление:
Напомним, что основная задача дифференциального исчисления заключается в следующем: по данной функции 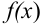 требуется найти её производную. Для дифференцирования существует обратная операция: нахождение первоначальной функции
требуется найти её производную. Для дифференцирования существует обратная операция: нахождение первоначальной функции 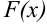 по известной производной
по известной производной 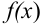 . Эта операция получила название интегрирование (от лат.
. Эта операция получила название интегрирование (от лат. 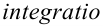 — восстановление).
— восстановление).
Так, попытаемся по известной производной 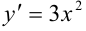 восстановить первоначальную функцию. Она будет иметь вид:
восстановить первоначальную функцию. Она будет иметь вид: 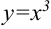 . Обозначим известную функцию
. Обозначим известную функцию 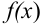 (в нашем примере
(в нашем примере 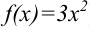 , а первоначальную функцию
, а первоначальную функцию 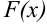 (в нашем примере
(в нашем примере 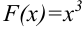 ). Функцию
). Функцию 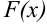 назовем первообразной данной функции
назовем первообразной данной функции 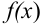 .
.
Функция 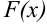 называется первообразной для функции
называется первообразной для функции 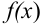 на интервале
на интервале 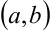 , если для всех
, если для всех  из этого промежутка справедливо равенство:
из этого промежутка справедливо равенство:
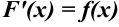 , или, что то же самое,
, или, что то же самое, 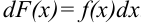 .
.
Пример №18.1.
Найдите какую-либо первообразную для функции 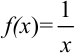 .
.
Решение:
Функция 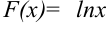 является первообразной для
является первообразной для 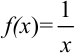 , т.к.
, т.к. 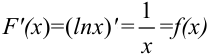 .
.
Нетрудно заметить, что первообразная 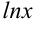 не является единственной для функции
не является единственной для функции 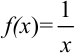 . В самом деле, в качестве первообразной можно было взять и функции
. В самом деле, в качестве первообразной можно было взять и функции 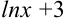 ,
, 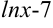 вообще
вообще 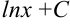 , где
, где 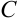 — произвольная постоянная, потому что
— произвольная постоянная, потому что 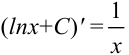 .
.
Приведём формулировку теоремы, выражающей основное свойство первообразных.
Теорема 1. Если функция 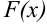 есть первообразная для функции
есть первообразная для функции 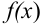 на некотором промежутке
на некотором промежутке 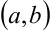 , то множество всех первообразных для
, то множество всех первообразных для 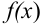 задается формулой:
задается формулой: 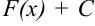 , где
, где 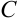 — константа.
— константа.
Множество всех первообразных для функции 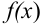 называется неопределённым интегралом от функции
называется неопределённым интегралом от функции 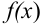 и обозначается символом
и обозначается символом 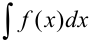 (читается: «интеграл от эф от икс де икс»).
(читается: «интеграл от эф от икс де икс»).
Таким образом, по определению 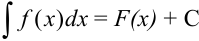 .
.
Функция 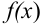 называется подынтегральной функцией,
называется подынтегральной функцией,
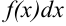 — подынтегральным выражением,
— подынтегральным выражением,
 — переменной интегрирования,
— переменной интегрирования,
символ 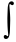 — знаком неопределённого интеграла.
— знаком неопределённого интеграла.
Пример №18.2.
Найдите 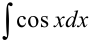 .
.
Решение:
Т.к. 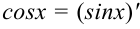 , то функция
, то функция 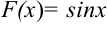 является одной из первообразных для функции
является одной из первообразных для функции 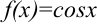 . Поэтому
. Поэтому 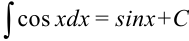 .
.
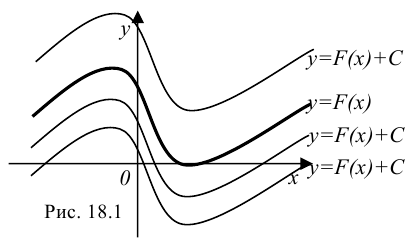
Геометрически неопределённый интеграл представляет собой семейство кривых, каждая из которых получается из любой другой параллельным переносом вдоль оси 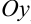 (рис. 18.1). График каждой первообразной называется интегральной кривой.
(рис. 18.1). График каждой первообразной называется интегральной кривой.
Встает вопрос: для всякой ли функции существует неопределенный интеграл? Справедлива следующая теорема:
Теорема 2. Всякая непрерывная на 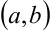 функция имеет на этом промежутке первообразную, а следовательно, и неопределённый интеграл.
функция имеет на этом промежутке первообразную, а следовательно, и неопределённый интеграл.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Алгоритм поиска асимптот |
| Общая схема исследования функции и построения графика |
| Основные свойства неопределенного интеграла. |
| Таблица основных интегралов. |

