Оглавление:




Понятие напряженного состояния в точке и его виды
- Понятие о стрессовом состоянии в какой-то момент Семя D9 Глава II получила формулу -COS2a, St • a TA = -sm2a Определение напряжения, действующего на участок, наклоненный к оси вытянутого или сжатого стержня. Из этих уравнений видно, что если наклон платформы, проходящей через какую-либо точку, изменится, то
нормальные и касательные напряжения OA и t, действующие на нее, также изменятся в сечении, проходящем под углом 45 ° к оси стержня. — В то же время видно, что максимальное поперечное напряжение возникает в поперечном сечении, а максимальное касательное напряжение. В более сложном случае воздействия
сил на перекладину также сложна проблема определения максимального Людмила Фирмаль
напряжения и положения платформы, на которую они действуют. Чтобы решить эту проблему, необходимо конкретно исследовать закон изменения напряжения при изменении наклона платформы через любую точку. Проблема изучения так называемых напряженных состояний возникает в терминах упругих тел.
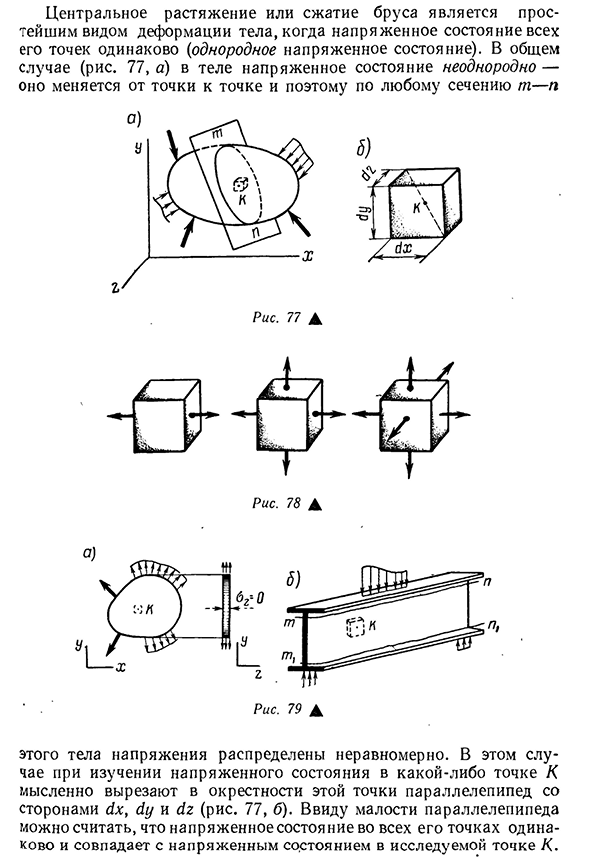
Напряженное состояние в определенный момент времени называется серией напряжений, которые воздействуют на все виды участков через эту точку. Концентрическое растяжение или сжатие стержня является самой простой формой деформации тела (состояние равномерного давления), когда условия давления во всех точках одинаковы. В общем случае (рис. 77, а) В теле напряженное состояние неоднородно и изменяется от точки к точке и, следовательно, по
- поперечному сечению tp. Рис 78А Рис 79А Это напряжение тела распределяется неравномерно. В этом случае при рассмотрении напряженного состояния в точке К рассекают мысленно в окрестностях этой точки стороны dx, dy и dz (рис. 77, б). Учитывая небольшой размер параллелепипеда, можно предположить, что напряженное состояние во всех точках одинаково и соответствует напряженному состоянию в исследуемой точке L. 85 По этой причине считается, что напряжение равномерно распределено как по лицу,
так и по его части. Считается, что эти предположения создают напряжение на плоскости параллелепипеда, что позволяет исследовать закон изменения напряжений для наклонной части основного параллелепипеда, как это сделано в § 9 для простого растяжения. Напряжение, действующее на наклонную область, определяется из метода перехвата, то есть из условия равновесия отрезанной части параллелепипеда. В будущем всегда можно выбрать базовый параллелепипед, чтобы в любой точке нагруженного
тела все грани были свободны от касательного напряжения, в этом случае точки являются линейными, Существуют плоские и объемные Людмила Фирмаль
напряженные состояния (рис. 78) в зависимости от того, испытывает ли параллелепипед одно, два или три напряжения (или сжатия) в перпендикулярном направлении друг к другу. Переживаю точку балки при центральном растяжении или сжатии. Условия напряжения самолета чаще всего замечены в материальных проблемах сопротивления. Его характеристики таковы: L l l l l l l l l x g R a n I x P A R l e l e l l e l i x g R a n I l l l l l l l l l l l n i x r i l l l l l n i x r Рассмотрим тонкую пластину под действием произвольной системы сил в плоскости, которая прикладывается к краю пластины (рис. 79, а). На поверхности пластины, параллельной плоскости Сюй,
отсутствует напряжение (ZG = 0). Поскольку толщина пластины мала, можно предположить, что она не находится внутри пластины в месте, параллельном этой поверхности. Следовательно, плоское напряженное состояние обычно существует в точке пластины. Описанные условия представляют собой, например, стержневые и балочные элементы, состоящие из относительно тонких пластин. Вертикальная стенка двутавровой балки (рис. 79, б), разделенная двумя продольными секциями t-p и WX-Px, нагружена в цепи
нормальной тангенциальной силой. Эта точка будет испытывать плоский стресс. Учитывая важность этого типа напряженного состояния для проблемы сопротивления материала, следующее основное внимание уделяется. Установите правило знака для напряжения в напряженном состоянии плоскости (рис. 80). Нормальное напряжение при растяжении считается положительным, сжатие — отрицательным. Если оно напряженное, касательное напряжение будет положительным. — G * Эти типы стрессовых состояний иногда называют одноосными, двухосными или трехосными соответственно. 86м можно вращать бесконечно малые
элементы корпуса по часовой стрелке, и наоборот. Отрежьте основной параллелепипед от пластины, как показано на рисунке. 79, вблизи любой точки / (сечение, перпендикулярное плоскости пластины. На части среды, окружающей параллелепипед, на него обычно воздействуют нормальные тангенциальные силы. Для риса. 81 эти силы Показывает векторы нормальных и касательных напряжений, соответствующие, что указывает на то, что все напряжения на грани параллелепипеда являются положительными. Отмечено, что напряженное состояние однородно во всех точках бесконечно малого параллелепипеда. В соответствии с этим,
напряжения с одинаковым названием (рис. 81) на параллельных гранях параллелепипедов показаны численно равными друг другу. Вам нужно обратить внимание на индекс при указании стресса. Касс Рис 80 £ рис. 81А Здесь первый индекс указывает, что вектор тангенциальных напряжений параллелен оси Y, а второй индекс является единственным индексом в обеих играх с индексом нормального напряжения, где это касательное напряжение перпендикулярно оси X. это. При анализе плоского напряженного состояния в точке напряжения av считается, что a, XH и XH заданы и называются начальными напряжениями.
Смотрите также:
| Решение практических задач при растяжении или сжатии | Закон парности касательных напряжений |
| Напряжения и деформации от собственного веса | Учет собственного веса и сил инерции |

