Оглавление:

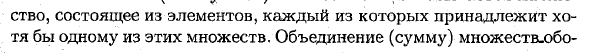






Понятие множества. Логические символы
- Многочисленные понятия. Логический символ Многие понятия являются одним из основных неопределенных понятий математики. Под набором понимают целостность некоторых объектов (коллекций, классов, семейств и т. Д.) На основе произвольных критериев. Таким образом, вы можете говорить о многих студентах в лаборатории, о многих рыбах в Черном море, о многих корнях формулы x’2 + 2a. + 2 = 0, набор всех натуральных чисел и т. Д.
Обычно наборы представлены латинскими заглавными буквами A, B, …, X, Y, … заглавными буквами, строчными буквами a, 6, …} x, y, … Представлено Если элемент x принадлежит множеству X, напишите x∈X ‘; запись x∈X или x∈X означает, что элемент x не принадлежит множеству X Набор, который не содержит ни одного элемента, называется пустым и обозначается символом 0. Элементы набора записаны в фигурных скобках, и они перечисляют элементы набора (если это возможно) или указывают общие свойства, принадлежащие всем элементам указанного набора.
Объекты, составляющие набор, называются его элементами. Людмила Фирмаль
Например, если вы пишете A = {1,3,15}, набор A состоит из трех чисел 1, 3 и 15. Обозначение A = {x: означает, что множество A состоит из всех действительных чисел, которые удовлетворяют неравенству 0 ^ x ^ 2 (если не указано иное). Если каждый элемент множества A является элементом множества B, множество A называется множеством множества B. Они говорят, что множества A и B равны или совпадают, и пишут A = B, если A C B и B C A. То есть множества, состоящие из одинаковых элементов, называются равными. Объединение (или сумма) множеств A и B называется множеством \ «‘1 свойство. Каждый элемент принадлежит хотя бы одному из этих наборов.
Средний AiB (или A + B). Проще говоря, вы можете написать AiB = {x: x 6 A или x G B}. Пересечение (или произведение) множества Aw B является множеством, состоящим из элементов, принадлежащих множеству A и множеству B соответственно. Пересечение (произведение) множества обозначается как A D) B (или A-B).
| Поверхности вращения, конические поверхности | Функция |
| Канонические уравнения поверхностей второго порядка | Последовательности |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Проще говоря, вы можете записать AR = {x: xbA и x 6 B}. В будущем мы будем использовать несколько простых логических символов для сокращения записей. a => ■ P-означает «из предложения следует предложение / 3». И 0- «a и f заявления эквивалентны». То есть оно следует из а в 0 и из р в а. V «-» означает «для всех» и «для всех». 3- «Существует», «Есть». : — «Беги», «Такой», б -> — «Соответствие». Пример: 1) Запись \ / x € A: a означает «Для всех элементов x € A предложение a сохраняется». 2) (i’6 / lu B) e L или x € B)] Эта запись Объединение множеств A и B 2. Числовой набор.
. Примеры наборов номеров: N = {1; 2; 3; …; n \ …} — множество натуральных чисел. = {0; 1; 2; …; n; …} — множество неотрицательных целых чисел Числа; Z = {0; ± 1; ± 2; …; ± p; …} — множество целых чисел. Q = | W-: m € Z, n € M j — множество рациональных чисел. R — это множество действительных чисел.
Много реальных чисел Набор, элементы которого являются числами, называется числом Людмила Фирмаль
Существует связь между этими наборами N C Z0. C Z C Q C R. >. Множество R содержит рациональные и иррациональные числа. Рациональное число представлено конечной дробью или бесконечной периодической дробью. Таким образом, A = 0,5 (= 0,500.,.), ^ = 0,333 … являются рациональными числами. Действительные числа, которые не рациональны, называются невозможными.
Теорема 1. Не существует рационального числа, квадрат которого равен 2. Предположим, что существует рациональное число, представленное M Неприводимая дробь — ее площадь равна 2. к (; J) 2 = 2>, т.е. m2 = 2n2. mn2 (и, следовательно, m) — четное число, то есть m = 2k. Подставив mn = 2k в уравнение m2 = 2n2, получим 4k2 = 27i2 или 2k2 = n2.
Число n четное, то есть n = 21. Однако доля ~ = U может быть уменьшена. Это противоречит предположениям, приведенным ниже, дроби неприводимы. Поэтому это не разумно 71 Число с квадратом, равным 2 ► Иррациональное число выражается в виде бесконечной апериодической дроби.
Следовательно, x / 2 = 1.4142356 …, tg = 3.1415926 … — иррациональное число. Мы можем сказать: набор действительных чисел — это набор десятичных знаков всех бесконечных десятичных знаков. И запиши E = {x: x = a, aza ^ az …}, a G Z, a * € {0,1, …, 9}. Вещественное множество R имеет следующие свойства: 1. Заказал. Для двух разных чисел a и b одно из двух соотношений имеет либо o 2a 2a <a + b <2b a << 2b). 3. Набор М непрерывен. Разбивает набор два на два Непустые классы A и B. Каждое действительное число содержится только в одном классе, и неравенство a c ^ 6 (Va ˆ A, V6 GB). Отдельный номер класса А от класса В. Число c является либо максимальным номером класса A (класс B не имеет минимального номера), либо минимальным номером класса B (класс A не имеет максимального номера).
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между каждым набором действительных чисел и каждым набором точек на линии. Это означает, что каждому числу x € K соответствует определенная (уникальная) точка на оси значений, и наоборот, конкретное (уникальное) действительное число соответствует точке на каждой оси
. Поэтому вместо слова «число» мы часто говорим «точка». 3. Числовой разрыв. Рядом с точкой Пусть a и b — действительные числа, а a a}; (-Oo; b) = {x: x <6}; (a, 4-й) = {rc: x> a}; (-Co, oo) = {x: —oo где E> 0 называется e-окрестностью точки x0, число x0 называется центром, а число e называется радиусом.хо хо хо хо х Для x 6 (xo-e; xo 4th) выполняется неравенство xq-e <x <xo + e или что такое же | x-x0 | <£. Неравенство | x-ho | <e означает, что точка x находится вблизи e от x

