Допустим, что существует такое число, квадрат которого равен -1. Обозначим его буквой 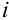 (от фран.
(от фран. 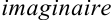 — мнимый) и будем называть мнимой единицей. Таким образом,
— мнимый) и будем называть мнимой единицей. Таким образом, 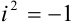 , а
, а 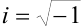 .
.
Введение мнимой единицы позволяет нам теперь извлекать квадратные корни даже из отрицательных чисел. Например, 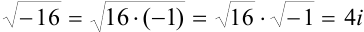 .
.
Рассмотрим степени мнимой единицы:
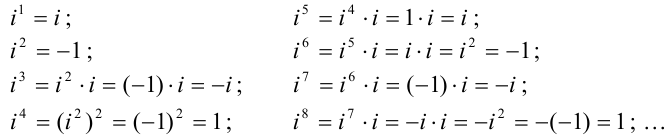
Легко заметить, что значения степеней числа 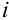 повторяются с периодом, равным четырем. Тогда для нахождения любой натуральной степени числа
повторяются с периодом, равным четырем. Тогда для нахождения любой натуральной степени числа 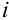 можно использовать следующие формулы (
можно использовать следующие формулы (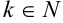 ):
):


Пример №42.1.
Вычислить: 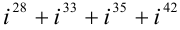 .
.
Решение:
Рассмотрим каждое слагаемое в отдельности.
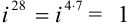 (если показатель степени числа
(если показатель степени числа 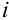 разделился на 4 без остатка, т.е.
разделился на 4 без остатка, т.е. 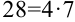 , то применяем формулу
, то применяем формулу 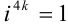 );
);
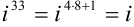 (по формуле
(по формуле 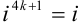 , в нашем случае
, в нашем случае 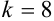 );
);
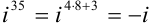 (по формуле
(по формуле 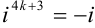 , в нашем случае
, в нашем случае 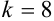 );
);
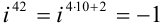 (по формуле
(по формуле 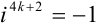 , в нашем случае
, в нашем случае 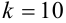 ).
).
Тогда 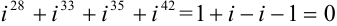 .
.
Ответ: 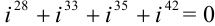 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

