Пусть функция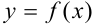 
имеет в точке 
отличную от нуля производную 
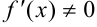. Это означает, что в точке существует предел 
.
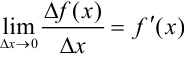Тогда используем теорему 1 о пределе функции (лекция 9): функцию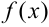 
, стоящую под знаком предела 
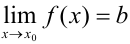, можно представить в ви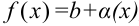де: 
, где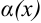 
— бесконечно малая функция при 
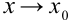(т.е.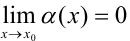 
).
Выражение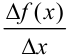 
, стоящее под знаком предела, можно записать как 
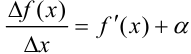, где 
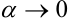при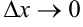 
.
Выразим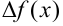 
из этого выражения: 
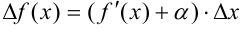или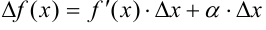 
.
Таким образом, приращение функции 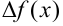представляет собой сумму двух слагаемых 
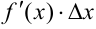и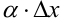 
. При этом второе слагаемое 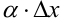стремится к нулю быстрее, чем 
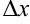, поэтому говорят, что 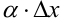есть бесконечно малая функция более высокого порядка, чем 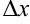. Следовательно, второе слагаемое практически не влияет на сумму. Поэтому первое слагаемое 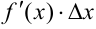называют главной частью приращения функции .
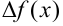Дифференциалом функции 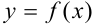в точке называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается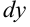 
(или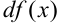 
): 
.
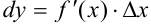Найдем дифференциал независимой переменной , для этого рассмотрим функцию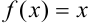 
. Воспользуемся определением дифференциала: 
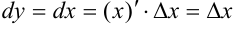, т.е. дифференциал независимой переменной равен приращению этой переменной: 
.
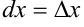Поэтому определение дифференциала функции можно записать так: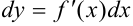 
. Итак, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы 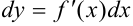следует равенство 
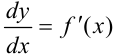. Теперь можно ввести новое обозначение производной: 
.
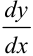Пример №12.3.
Найдите дифференциал функции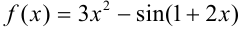 
.
Решение:
По формуле 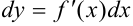находим:
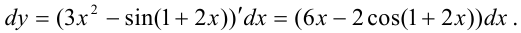
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Геометрический смысл производной. |
| Уравнение касательной к кривой. |
| Геометрический смысл дифференциала. |
| Понятие производной высших порядков |
