Оглавление:
Понятие числовой последовательности
Определение 2.1. Если каждому натуральному числу 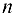 поставлено в соответствие число
поставлено в соответствие число 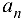 , то говорят, что задана числовая последовательность или просто последовательность
, то говорят, что задана числовая последовательность или просто последовательность 
Числа 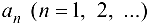 — элементы или члены последовательности,
— элементы или члены последовательности, 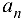 — общий или
— общий или 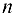 -й член последовательности. Последовательность обозначают как
-й член последовательности. Последовательность обозначают как 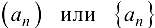 или задают с помощью
или задают с помощью 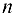 -го члена.
-го члена.
Частным случаем последовательности являются арифметическая и геометрическая прогрессии.
Пример 2.1.
а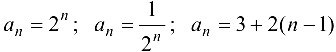
Определение 2.2. Последовательность называется ограниченной, если существуют такие числа 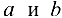 , что при всех
, что при всех 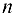 выполняются неравенства
выполняются неравенства
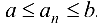
При этом говорят, что число 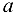 ограничивает последовательность снизу, a
ограничивает последовательность снизу, a 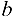 — сверху.
— сверху.
Определение 2.2′. Последовательность 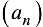 называется ограниченной, ест
называется ограниченной, ест 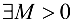 такое, что для
такое, что для 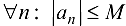
Заметим, что не всякая последовательность ограничена.
Пример 2.2.
Последовательность 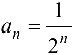 ограничена снизу 0, сверху
ограничена снизу 0, сверху 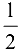 ; последовательность
; последовательность 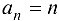 ограничена снизу 1.
ограничена снизу 1.
Определение 2.3. Последовательность 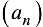 называется неограниченной, если для
называется неограниченной, если для 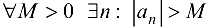
Пример 2.3.
Последовательность 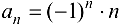 не ограничена.
не ограничена.
Если изображать члены последовательности точками координатной прямой, то все члены ограниченной последовательности лежат на некотором отрезке. Для неограниченной последовательности вне любого отрезка найдутся члены этой последовательности.
Определение 2.4. Если из некоторого бесконечного подмножества членов последовательности 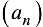 образована новая последовательность, порядок следования членов в которой такой же, как и в
образована новая последовательность, порядок следования членов в которой такой же, как и в 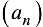 , то опа называется подпоследовательностью
, то опа называется подпоследовательностью 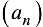 и обозначается
и обозначается 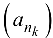 , причем
, причем 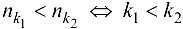 .
.
Определение 2.5. Суммой, разностью, произведением, отношением последовательностей 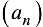 и
и 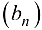 называют последовательности
называют последовательности 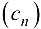 , члены которых образованы по следующим правилам:
, члены которых образованы по следующим правилам: 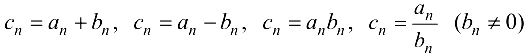 . Произведением последовательности
. Произведением последовательности 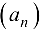 на число С называется последовательность
на число С называется последовательность 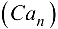 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

