Оглавление:
Пусть  — некоторая функция двух действительных переменных. Частные производные
— некоторая функция двух действительных переменных. Частные производные 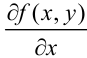 и
и 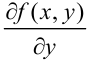 называют частными производными первого порядка. Частные производные первого порядка, вообще говоря, сами являются функциями двух действительных переменных. Поэтому для них также можно вычислять частные производные. По отношению к исходной функции эти производные от частных производных называются частными производными второго порядка. Итак, частная производная от частной производной первого порядка называется частной производной второго порядка. Функция
называют частными производными первого порядка. Частные производные первого порядка, вообще говоря, сами являются функциями двух действительных переменных. Поэтому для них также можно вычислять частные производные. По отношению к исходной функции эти производные от частных производных называются частными производными второго порядка. Итак, частная производная от частной производной первого порядка называется частной производной второго порядка. Функция  двух действительных переменных имеет четыре частных производных второго порядка. Они определяются и обозначаются следующим образом:
двух действительных переменных имеет четыре частных производных второго порядка. Они определяются и обозначаются следующим образом:
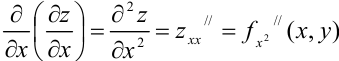 — частная производная второго порядка функции
— частная производная второго порядка функции  по переменной
по переменной  ;
;
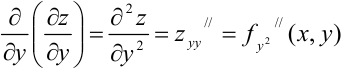 — частная производная второго порядка функции
— частная производная второго порядка функции  по переменной
по переменной  ;
;
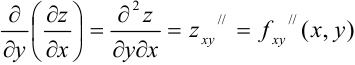 — частная производная второго порядка функции
— частная производная второго порядка функции  по переменным
по переменным  и
и  ;
;
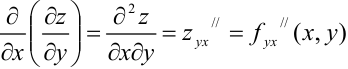 — частная производная второго порядка функции
— частная производная второго порядка функции  по переменным
по переменным  и
и  .
.
Рассматривая частные производные от частных производных второго порядка, получим всевозможные частные производные третьего порядка. Например, 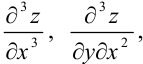
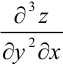 и т.д.
и т.д.
Аналогично определяются частные производные произвольного (высшего) порядка.
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например, 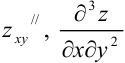 .
.
Пример №27.1.
Найдите частные производные второго порядка функции 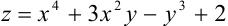 .
.
Решение:
Найдем частные производные первого порядка функции:
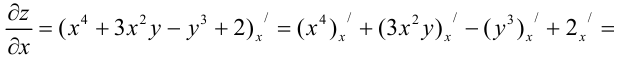
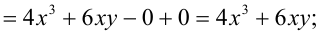
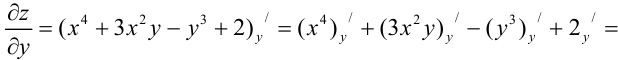
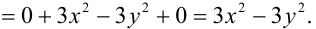
Найдем 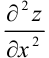 как частную производную по переменной
как частную производную по переменной  от
от 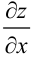 :
:
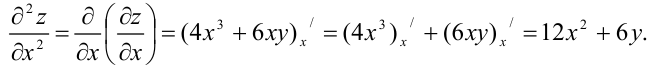
Найдем 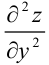 как частную производную по переменной
как частную производную по переменной  от
от 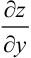 :
:
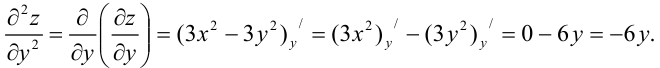
Найдем 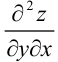 как частную производную по переменной
как частную производную по переменной  от
от 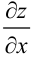 :
:
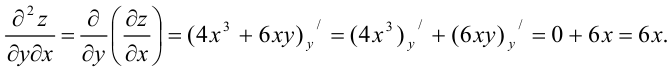
Найдем 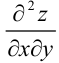 как частную производную по переменной
как частную производную по переменной  от
от 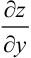 :
:
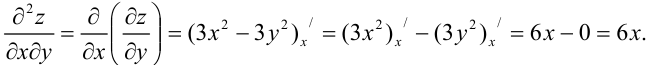
Ответ: 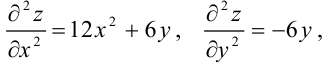
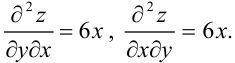
Анализируя пример 27.1, обратим особое внимание на равенство смешанных производных второго порядка: 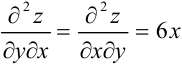 . Оказывается, что значения смешанных производных второго порядка не зависят от того, дифференцируем мы функцию
. Оказывается, что значения смешанных производных второго порядка не зависят от того, дифференцируем мы функцию  сначала по переменной
сначала по переменной  , а затем — по
, а затем — по  , или наоборот. Этот результат нс случаен. Имеет место теорема, которую мы рассмотрим без доказательства.
, или наоборот. Этот результат нс случаен. Имеет место теорема, которую мы рассмотрим без доказательства.
Теорема (Шварца). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, если вторые производные непрерывны, то для  имеем:
имеем:
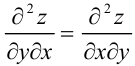
Пример №27.2.
Найдите смешанные производные второго порядка функции 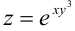 .
.
Решение:
Воспользуемся теоремой Шварца о равенстве смешанных производных второго порядка: 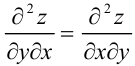 и найдем только одну смешанную производную, например,
и найдем только одну смешанную производную, например, 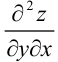 .
.
Найдем частную производную первого порядка функции по переменной  :
:
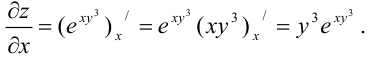
Найдем 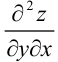 как частную производную по переменной
как частную производную по переменной  от
от 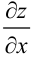 :
:
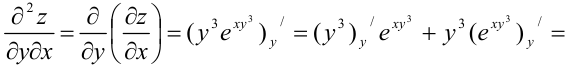
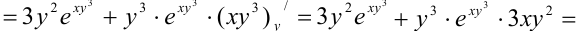
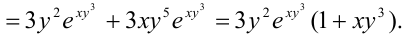
Ответ: 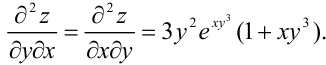
Пример №27.3.
Найдите частные производные третьего порядка функции 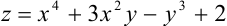 из примера 27.1.
из примера 27.1.
Решение:
Функция  двух действительных переменных имеет восемь частных производных третьего порядка:
двух действительных переменных имеет восемь частных производных третьего порядка:
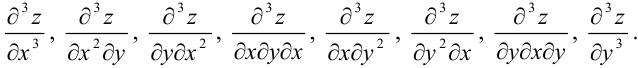
Но по теореме Шварца получаем следующие равные смешанные производные третьего порядка:
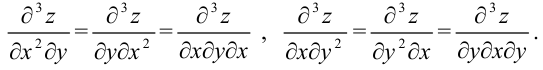
Следовательно, фактически надо найти четыре частные производные третьего порядка:
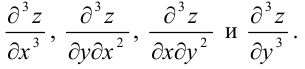
Для этого будем использовать частные производные второго порядка 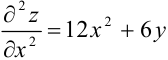 и
и 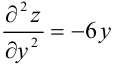 , полученные нами в примере 27.1.
, полученные нами в примере 27.1.
Найдем 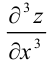 как частную производную по переменной
как частную производную по переменной  от
от 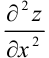 :
:
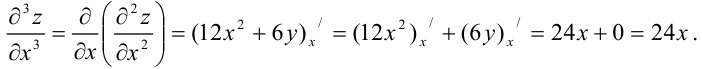
Найдем 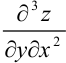 как частную производную по переменной
как частную производную по переменной  от
от 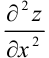 :
:
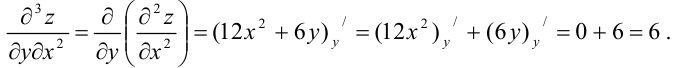
Найдем 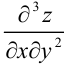 как частную производную по переменной
как частную производную по переменной  от
от 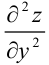 :
:
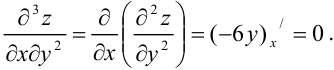
Найдем 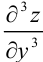 как частную производную по переменной
как частную производную по переменной  от
от 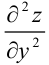 :
:
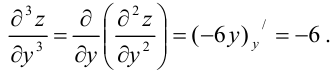
Ответ: 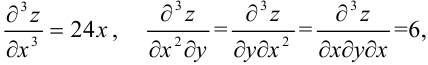
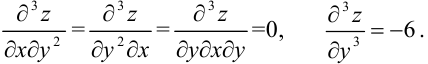
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

