Рассмотрим функцию  , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки 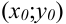 . При фиксированном значении переменной
. При фиксированном значении переменной  , например
, например 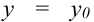 , функция
, функция 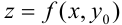 окажется уже функцией только от одной переменной
окажется уже функцией только от одной переменной  . Таким образом, совершенно естественно возникает вопрос о построении дифференциального исчисления для функций двух действительных переменных аналогично случаю функции одной действительной переменной.
. Таким образом, совершенно естественно возникает вопрос о построении дифференциального исчисления для функций двух действительных переменных аналогично случаю функции одной действительной переменной.
Придадим независимой переменной 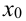 приращение
приращение 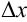 , оставляя значение
, оставляя значение 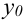 неизменным (другими словами, перейдем от точки
неизменным (другими словами, перейдем от точки 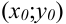 к точке
к точке 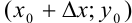 ). Тогда функция
). Тогда функция  получит приращение
получит приращение 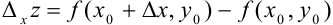 , называемое частным приращением функции в точке
, называемое частным приращением функции в точке 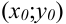 по переменной
по переменной  . Распространим определение производной функции одной действительной переменной на случай функции двух переменных.
. Распространим определение производной функции одной действительной переменной на случай функции двух переменных.
Частной производной функции двух переменных  по переменной
по переменной  в точке
в точке 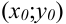 называется существующий предел отношения частного приращения функции в этой точке по переменной
называется существующий предел отношения частного приращения функции в этой точке по переменной  к приращению этой переменной при условии, что последнее стремится к нулю:
к приращению этой переменной при условии, что последнее стремится к нулю:
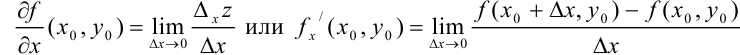
Для частной производной функции  по переменной
по переменной  часто используются другие обозначения:
часто используются другие обозначения: 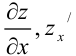 .
.
Аналогично определяется и обозначается частная производная функции двух переменных  по переменной
по переменной  в точке
в точке 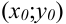 :
:
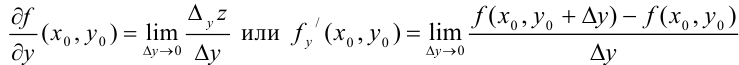
Таким образом, частная производная функции двух переменных определяется как производная функции одной из этих переменных при условии постоянства значений другой переменной. Аналогично определяются частные производные функции трех и более переменных. Поэтому техника нахождения частных производных ничем не отличается от обычного дифференцирования, нужно только помнить, что при дифференцировании функции по какой — либо переменной все остальные переменные принимаются за постоянные.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
