Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций 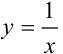 ,
, 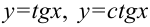 . Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.
. Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.
Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.
Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:
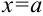 — вертикальная асимптота
— вертикальная асимптота
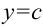 — горизонтальная асимптота
— горизонтальная асимптота
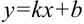 — наклонная асимптота
— наклонная асимптота
Дадим определение каждому виду асимптот:
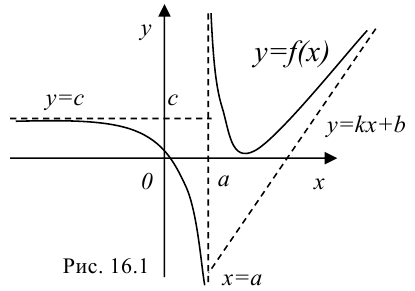
- Прямая
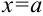 называется вертикальной асимптотой функции
называется вертикальной асимптотой функции 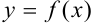 , если
, если 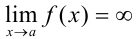 .
. - Прямая
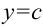 называется горизонтальной асимптотой функции
называется горизонтальной асимптотой функции 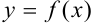 , если
, если 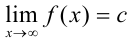 .
. - Прямая
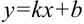 называется наклонной асимптотой функции
называется наклонной асимптотой функции 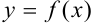 , если
, если 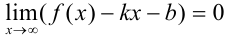 .
.
Геометрически определение наклонной асимптоты означает, что при 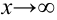 график функции
график функции 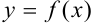 сколь угодно близко подходит к прямой
сколь угодно близко подходит к прямой 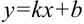 , т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.
, т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.
Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии 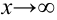 . Иногда их различают на горизонтальные и наклонные асимптоты при
. Иногда их различают на горизонтальные и наклонные асимптоты при 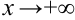 и
и 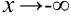 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие выпуклой и вогнутой функции |
| Критерий выпуклости-вогнутости функции и точек перегиба. |
| Алгоритм поиска асимптот |
| Общая схема исследования функции и построения графика |
