Арифметическая (обыкновенная) дробь — это число, составленное из целого числа долей единицы. Дробь изображается символом p/q, где р — числитель дроби, он показывает число взятых долей единицы и делится на столько долей, сколько показывает (знаменует) знаменатель q. Дробь можно рассматривать как частное от деления одного (целого) числа р на другое (натуральное) q .
В старину в России дроби назывались ломаными числами (например, в «Арифметике» Магницкого и в «Недоросле» Фонвизина).
Обыкновенная дробь р /q называется правильной, если её числитель по модулю меньше знаменателя, или |p/q| < 1, и неправильной в противном случае (понятие модуля будет введено в разделе 2). Неправильная дробь может быть представлена в виде суммы целого числа и правильной дроби (смешанная дробь). Для этого надо числитель разделить (с остатком) на знаменатель. Например,
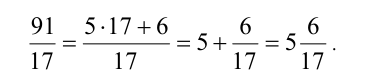
Обыкновенную дробь называют сократимой, если существует такое отличное от единицы натуральное число n , что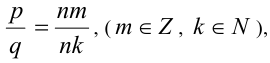 
и несократимой, если |p| и q— взаимно простые числа. Любую сократимую дробь путём сокращения числителя и знаменателя на их общие делители можно привести к несократимому виду.
Две дроби называют равными, если их несократимые представления совпадают. Например, дроби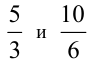 
равны между собой. Отсюда получаем как следствие: при умножении числителя и знаменателя дроби одновременно на одно и то же число получается дробь, равная данной.
Это даёт возможность любые две дроби привести к общему знаменателю, т.е. найти соответственно равные им дроби, знаменатели которых совпадают. При этом наименьшим общим знаменателем для двух данных дробей будет, очевидно, наименьшее общее кратное их знаменателей (в несократимых представлениях). Аналогичным образом можно приводить к общему знаменателю три дроби и более.
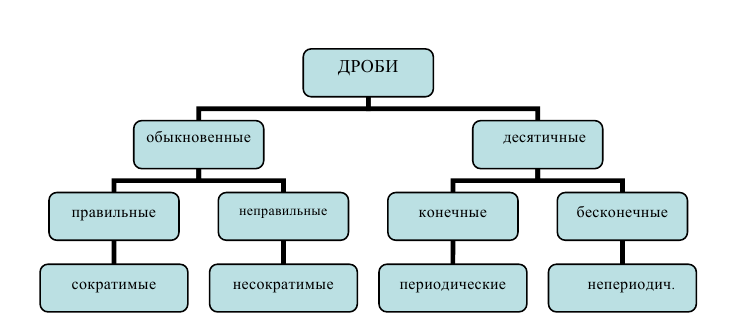
Дробь p/q называется десятичной, если её знаменатель q является натуральной степенью числа 10. Для десятичной дроби используется запись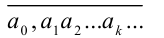 
(черту сверху часто опускают), где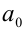 
— целое число, а 
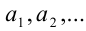— цифры, принимающие значения 
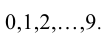Например, вместо 
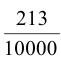пишут 
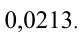Десятичные дроби, имеющие после запятой конечное число ненулевых цифр, называются конечными. В противном случае дробь считается бесконечной.
Бесконечные десятичные дроби разбиваются на два класса: периодические, когда, начиная с некоторого момента, одна и та же группа цифр неограниченно повторяется, и непериодические, если не существует такой бесконечно повторяющейся группы цифр после запятой. Повторяющуюся группу цифр после запятой называют периодом и заключают в круглые скобки. Например, вместо 0,2353535… пишут 0,2(35). Читается: «ноль целых, две десятых и тридцать пять в периоде».
Если число 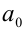в записи десятичной дроби 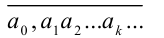является натуральным, то такая дробь называется положительной. Если число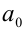— целое отрицательное, то в этом случае десятичная дробь называется отрицательной. Если 
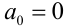и хотя бы одна из цифр после десятичной запятой отлична от нуля, то соответствующую десятичную дробь также относят к положительным дробям. Если же в последнем случае перед такой дробью поставить знак «минус», то получим отрицательную десятичную дробь. Если среди 
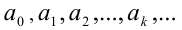нет чисел, отличных от нуля, то такое число называют нулевой бесконечной периодической дробью и обозначают 0,(0).
Операции над дробями встречаются уже в древнеегипетском папирусе Ахмеса (ок. 2000 г. до н.э.). У древних индийцев, по-видимому, впервые зародилось современное обозначение дробей. Термин «дробь» вошел в европейскую математику от арабов через Леонардо Пизанского (1202), термины «числитель» и «знаменатель» встречаются у Максима Плануда (конец XIII века). Однако изложение обыкновенных дробей в учебниках арифметики европейских школ произошло только в XVIII в. Дроби усваивались учениками с огромными трудностями. Например, в предисловии к 16-му изданию «Арифметики» Уингейта (Англия) сказано, что в этом издании «изложение арифметики целых чисел, необходимой для денежных расчётов, для торговли и других приложений, даётся раньше, чем открывается доступ к крутым и трудным путям дробей, при одном виде которых некоторые учащиеся приходят в такое уныние, что останавливаются и восклицают: ради бога, не дальше!». Даже в знаменитой Итонской школе для аристократов, существующей с 1446 г., арифметика стала обязательным предметом преподавания только в 1851 г.
Пример. Доказать, что дробь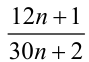 
— несократима при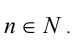 
Доказательство. 1-й способ (по определению сократимой дроби). Предположим, от противного, что данная дробь сократима на некоторое натуральное число р , отличное от единицы. Тогда найдутся такие натуральные числа m и k , что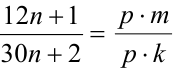 
, т.е. выполняется система двух равенств
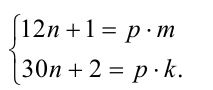
Исключим из уравнений системы величину n. Для этого умножим первое равенство на 5, второе на 2 и вычтем из первого второе:
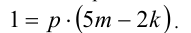
Проанализируем полученное равенство. В правой его части стоит произведение двух целочисленных множителей: р и 5m — 2k, а слева — единица. Понятно, что в этой ситуации р может принимать только значение, равное единице. Полученное противоречие означает, что предположение о сократимости дроби было неверным.
2-й способ. При этом способе решения используются два очевидных утверждения: во-первых, дроби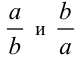 
— (при натуральных а,b) сократимы или несократимы одновременно; во-вторых, дробь 
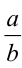и та дробь, которая получается из неё после выделения целой части, также одновременно сократимы либо несократимы. Итак, дробь
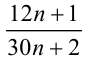— сократима (несократима) одновременно с персвсрнутой» дробью 
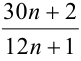. Выделим в этой дроби целую часть:
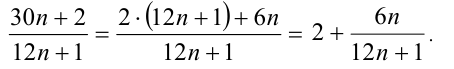
Тогда дробь 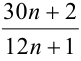— сократима (несократима) одновременно с дробью 
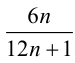, а она, в свою очередь, с дробью 
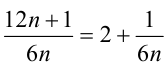. Таким образом, задачу исследования на сократимость исходной дроби свели к аналогичной задаче для более простой дроби 1/(6n), которая, очевидно, является несократимой при натуральных n .
3-й способ. Используя последовательно свойство «Если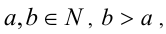 
то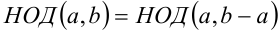 
», вычислим
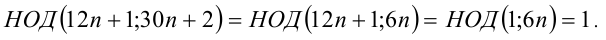
Таким образом, числитель и знаменатель дроби являются взаимно простыми числами, следовательно, данная дробь несократима.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
