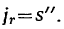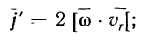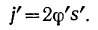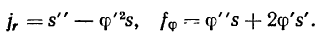Задача №20.
Пользуясь теоремой Кориолиса, определим ускорение материальной точки в полярной системе координат. Воспользуемся следующей схемой. Пусть движение -материальной точки 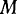 по палочке
по палочке 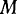 «происходит то произвольному закону
«происходит то произвольному закону 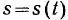 (рис. 63). Будем предполагать, что палочка вращается
(рис. 63). Будем предполагать, что палочка вращается
в своей плоскости вокруг неподвижного конца  , причем угол
, причем угол 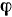 , который она образует с некоторой неподвижной прямой этой плоскости, изменяется по произвольному закону
, который она образует с некоторой неподвижной прямой этой плоскости, изменяется по произвольному закону 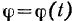
Решение:
Для определения ускорения материальной точки воспользуемся теоремой Кориолиса. Здесь в переносном движении материальная точка 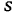 движется по окружности радиуса с центром в точке
движется по окружности радиуса с центром в точке  . Определяя переносное ускорение, мы обязаны положить
. Определяя переносное ускорение, мы обязаны положить 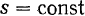 . Тогда получим две составляющих переносного ускорения:
. Тогда получим две составляющих переносного ускорения:
Относительное движение материальная точка совершает по прямой 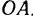 . Следовательно, относительное ускорение будет направлено вдоль палочки, а его величина равна
. Следовательно, относительное ускорение будет направлено вдоль палочки, а его величина равна
Добавочное ускорение получим из формулы
оно будет направлено ортогонально к палочке в сторону вращения, а по величине равно
Проектируя вектор ускорения на направление палочки и на ортогональное к ней направление (см. рисунок), получим так называемые радиальную и трансверсальную составляющие ускорения:
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №18. По неподвижному круговому конусу с углом при вершине, равным , катится без скольжения другой круговой конус с углом при вершине, равным , так, что ось симметрии последнего вращается вокруг оси симметрии не-подвижного конуса с постоянной угловой скоростью ooj. Определить абсолютную угловую скорость вращения подвижного конуса и найти аксоиды. |
| Задача №19. Горизонтальные колеса I и II дифференциального механизма вращаются вокруг одной и той же вертикальной оси соответственно со скоростями и . Определить мгновенную угловую скорость вращения планетного колеса III, ось которого может свободно вращаться вокруг оси (рис. 60). |
| Задача №21. Палочка длины а скользит своими концами и по неподвижным вертикальной и горизонтальной прямым так, что ее конец движется с постоянной скоростью (рис. 64). По палочке движется материальная точка с постоянной относительной скоростью . Определить абсолютное ускорение материальной точки , принимая в качестве параметра, определяющего положение палочки, угол , который она образует с вертикалью. |
| Задача №22. Окружность радиуса (рис. 65) вращается в своей плоскости вокруг своей неподвижной точки с постоянной угловой скоростью против часовой стрелки. Стержень вращается в той же плоскости вокруг точки с постоянной угловой скоростью по часовой стрелке. На стержень и на окружность надето колечко . Определить скорость и ускорение колечка в зависимости от ее-личины угла , который образует радиус окружности со стержнем. |

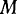 по палочке
по палочке 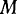 «происходит то произвольному закону
«происходит то произвольному закону 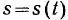 (рис. 63). Будем предполагать, что палочка вращается
(рис. 63). Будем предполагать, что палочка вращается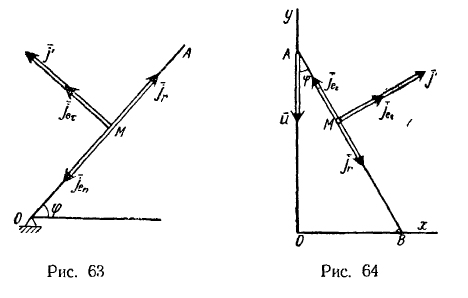
 , причем угол
, причем угол 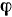 , который она образует с некоторой неподвижной прямой этой плоскости, изменяется по произвольному закону
, который она образует с некоторой неподвижной прямой этой плоскости, изменяется по произвольному закону 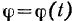
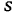 движется по окружности радиуса с центром в точке
движется по окружности радиуса с центром в точке  . Определяя переносное ускорение, мы обязаны положить
. Определяя переносное ускорение, мы обязаны положить 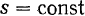 . Тогда получим две составляющих переносного ускорения:
. Тогда получим две составляющих переносного ускорения:
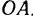 . Следовательно, относительное ускорение будет направлено вдоль палочки, а его величина равна
. Следовательно, относительное ускорение будет направлено вдоль палочки, а его величина равна