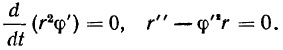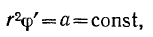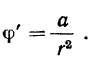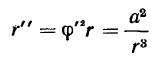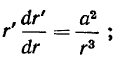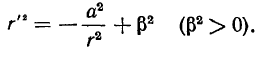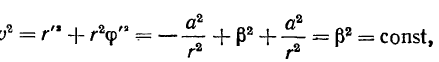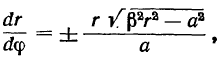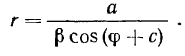Задача №9.
Пользуясь формулами для ускорения точки о полярной системе координат, доказать, что если ускорение точки равно нулю, точка будет совершать равномерное и прямолинейное движение.
Решение:
Очевидное решение задачи совсем непросто получить, пользуясь только полярной системой отсчета. В самом деле, в этом случае будем иметь
Отсюда следует, что
то есть
Далее
или
интегрируя это уравнение, получим
Подставляя полученное значение в выражение скорости в полярной системе координат, будем иметь
что говорит о движении точки с постоянной по величиие скоростью.
С другой стороны, имеем
откуда, интегрируя, получим
Последнее уравнение является уравнением прямой линии в полярной системе координат, чем и доказывается утверждение.
В качестве упражнений па применение полярной системы координат и естественных осей предлагается решить следующие задачи.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №7. Точка движется по винтовой линии с постоянной по величине скоростью . Определить величину и направление ускорения и радиус кривизны траектории точки. |
| Задача №8. Точка описывает плоскую кривую. Радиальная составляющая скорости точки положительна и постоянна по величине, а радиальная составляющая ускорения отрицательна и обратно пропорциональна кубу расстояния от некоторого полюса. Определить траекторию и секторную скорость точки. |
| Задача №10. Плоская материальная кривая, уравнение которой, отнесенное к подвижной системе отсчета, имеет вид , движется в своей плоскости поступательно справа налево с постоянной скоростью . Палочка , длина которой равна , шарнирно закреплена одним концом в неподвижной точке и опирается на эту кривую другим (свободным) концом. Определить угловую скорость палочки в зависимости от положения системы (рис. 13). |
| Задача №11. Палочка длины а вращается в плоскости чертежа вокруг неподвижной точки с постоянной угловой скоростью (рис. 14). Вокруг подвижного конца этой палочки в той же плоскости вращается другая палочка длины так, что угол , заключенный между палочками, изменяется по закону где постоянна по величине. Определить абсолютную скорость точки , применяя теорему о сложении скоростей. |