Задача №25.
Полый цилиндр радиуса 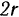 вращается вокруг своей неподвижной оси симметрии с постоянной угловой скоростью
вращается вокруг своей неподвижной оси симметрии с постоянной угловой скоростью 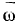 . По внутренней поверхности этого цилиндра катится без скольжения другой цилиндр радиуса
. По внутренней поверхности этого цилиндра катится без скольжения другой цилиндр радиуса 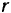 с постоянной относительной угловой скоростью
с постоянной относительной угловой скоростью 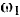 (как показано на рис. 67). Определить ускорение точки
(как показано на рис. 67). Определить ускорение точки 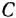 малого цилиндра, совпадающей в рассматриваемый момент времени с осью большого.
малого цилиндра, совпадающей в рассматриваемый момент времени с осью большого.
Решение:
Выберем за полюс точку 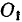 . Скорость точки
. Скорость точки 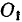 может быть получена как скорость точки в сложном движении, где переносная скорость равна
может быть получена как скорость точки в сложном движении, где переносная скорость равна  ,а относительная скорость равна
,а относительная скорость равна 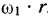 . Тогда абсолютная скорость точки
. Тогда абсолютная скорость точки 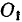 будет по величине равна
будет по величине равна
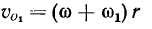
и направлена в сторону вращения полого цилиндра. Точка 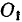 движется по окружности радиуса
движется по окружности радиуса 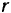 с постоянной по величине скоростью
с постоянной по величине скоростью 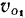 . Благодаря этому ускорение полюса по величине
. Благодаря этому ускорение полюса по величине
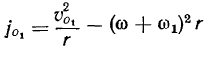
и направлено к точке 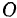 . Для определенности положим
. Для определенности положим  . Тогда абсолютная угловая скорость малого колеса будет равна
. Тогда абсолютная угловая скорость малого колеса будет равна
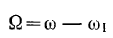
и направлена против часовой стрелки. По величине  остается постоянной во все время движения. Поэтому угловое ускорение будет равно нулю. Ускорение точки
остается постоянной во все время движения. Поэтому угловое ускорение будет равно нулю. Ускорение точки  колеса складывается из ускорения точки
колеса складывается из ускорения точки  и из нормального ускорения
и из нормального ускорения
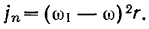
Проектируя на направление  получим
получим

откуда видно, что ускорение направлено от точки  .
.
При решении пространственных задач необходимо помнить, что вектора  и
и 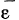 вообще не совпадают по направлению. Это обстоятельство создает некоторые осложнения при решении задач. Рассмотрим следующие задачи.
вообще не совпадают по направлению. Это обстоятельство создает некоторые осложнения при решении задач. Рассмотрим следующие задачи.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

