Оглавление:












Полярные координаты
- Полярная система координат it01.Полярная система координат. Ранее для определения положения точки на плоскости мы использовали ее декартовы координаты. Далее, подумайте о другой важной системе координат 1: полярные координаты. Эта система состоит из оси Ox (полюса), которая проходит через определенную точку O (полюса)
To для этого соедините точку M с полюсом O и найдите угол, под которым образуется луч OM в положительном направлении оси полюса Ox и длину этого луча r) OM (рис. 80). Числа b и d называются радиус-векторами
и оси*).Используя спецификации Объект может определить положение любой точки G. Людмила Фирмаль
аргументов и точек M соответственно. Их общее название-полярные координаты этой точки. Тот факт, что точка M имеет полярные координаты изгиба, обычно описывается в виде M (r, 6).Это барахтанье не было очень успешным.、 Рисунок 80. * ) Ось-это линия, в которой выбрано положительное направление. Поэтому мы говорили об осях Ох и Oy ранее. •* ) Конечно, Луч
представляет собой бесконечную полулинию, поэтому он означает длину отрезка олух. Поскольку значение символа M (3, 2) не ясно, точки, где абсцисса и ордината будут равны 3 и 2 соответственно, или точки, где эти числа будут радиус-вектором и arguments. In в последующей части книги эта двусмысленность устраняется сопроводительным описанием, и в этом разделе мы вводим
- обозначение M (r, 0), но оно вообще не принято. Полярная система координат имеет некоторые недостатки по сравнению с прямоугольником. Прежде всего, любое число можно считать аргументом для поляков. * ), A (0, 1>, B (0, −10), C (0, 42°) — различные обозначения одной и той же точки (полюса).кроме того, другие точки на плоскости имеют бесконечное число
аргументов. Это связано с тем, что добавление к аргументу угловой точки 2mc = 360°не меняет этого point. So, M (5, 73°), N <5, 443°), P (5, 803°), Q <5, −287°) представляют одни и те же точки. Можно также рассмотреть радиус-вектор отрицательного значения. Например, это означает точку на M (-2, 60°) (рис. 81)、 81. Это
Расстояние между 2 точками. Проблема. Людмила Фирмаль
получается в результате следующей композиции: сначала поверните ось полюса на 60°(всегда против часовой стрелки).Затем на оси (в новом положении! Положите в отрицательном направлении сегмент 2).Результирующей точкой будет точка M (-2, 60°).Однако нетрудно понять, что ту же самую точку M можно описать как: M {2, 240°).То есть, вы можете установить те же точки, используя положительные значения радиус-вектора. Аналогично, если
вы добавляете 180°к аргументу, вы всегда можете изменить отрицательный радиус-вектор на положительный радиус-вектор. Имея это в виду, я соглашусь только один раз рассмотреть радиус-вектор r неотрицательной точки r ^ rO. н°2. Найти расстояние d между точками Mi (ru 6) и Mg(r * 0i). Угол 2 * •* ) Конечно, равенство 2 * = 360е Радианы равны.
Угол 360″*.Таким образом, в данном равенстве нельзя рассматривать левую сторону как абстрактное число(то же, что и равенство 1 м = \ 00 см Уравнение 1 = 100 см заменить нельзя).Такие как Внешний вид х = 180 * Это связано с тем, что имя»Радиан«обычно опускается, устанавливая угол в радианах с соответствующей спецификацией. •) В точке M(2,3) аргумент равен 3 радианам, а в точке N (2,3) — 3 градусам. П°3.Связь между полярными и Декартовыми
координатами. Создайте 2 системы координат на плоскости.1-й полюс и полюсные оси-это полюсы и прямоугольники, соответствующие 2-му началу координат и абсциссе. Я возьму его. Solution. By по теореме косинусов из треугольника OAfjM(рис. 82)、 д = ут + РЖ-2р, потому что Р9(9 с-0j). Рисунок 83. Диаграмма 82. (2) Возьмем любую точку M на плоскости (рис. 83), ее полярные и декартовы координаты (x, y) и (r, b) соответственно. Как видно из треугольника ОМА, формула
верна х = tcosO, ЕУ = rsin б、 Представляет декартовы координаты в полярных координатах. Формула (2) может оказаться верной, как и простейшее положение точки Af, показанное на рисунке. 83, но и в любой из своих позиций. Однако мы не будем это обсуждать. Уравнение (2) (или непосредственно из треугольника ОМА)、 Р = У1?Орр (3)) Радикальное заявление для нас (4 )) В Формуле (4) Вы не можете найти угол 0 в x и y. это связано с тем, что угол не может быть определен четко по касательной. Но если вы знаете x и y、
Кроме того, согласно вышесказанному, всегда используйте 4 минуты 1, где угол b существует, можно объединить с формулой (4), чтобы найти b с точностью до 360 градусов. о°4.Спираль Архимеда. Мы знаем, что различные линии на плоскости определяются с помощью уравнений, которым должны соответствовать декартовы координаты точек линий. Но если речь идет не о прямоугольниках,
а о полярных координатах точек, то ровно столько же applies. It удобнее изучать прямые линии, эллипсы, параболы и гиперболы в уравнениях декартовых координат. Однако для некоторых линий уравнения в полярных координатах являются более удобным средством обучения. Такие линии, например, являются спиралями
Архимеда. Определение спираль Архимеда-это линия, описываемая точкой, которая равномерно движется вдоль луча, который равномерно вращается вокруг начала координат. — Предположим, что точка M в первый момент, представляющая собой спираль, находится в начале луча, упомянутого в определении. Вытекает
уравнение arcimedes спирали. Для этого необходимо сначала выбрать определенную систему координат. Для полюсов используйте начало луча, в котором движется точка M, а для положительного направления оси полюса-начальное положение этого луча. «Скорость вращения луча и скорость-движение точки м вдоль луча» представлена щитом. Поскольку оба движения одинаковы, то есть угол, под которым луч вращается в единицу времени, v — это
расстояние за единицу времени, которое точка M, представляющая собой спираль, проходит вдоль луча. Положение точки M определяется ее полярными координатами r и B. В первый момент r = 0 =0.At то же время(то есть в момент отрыва на t от первого временного интервала)) Вопрос-ут, Р = Вт. Следовательно, в любой момент времени t g_ _ в_ е-« (Константа! Указать кол-КТ показывает, что уравнение arcimedes спираль имеет форму: Р = АО. Поэтому, когда
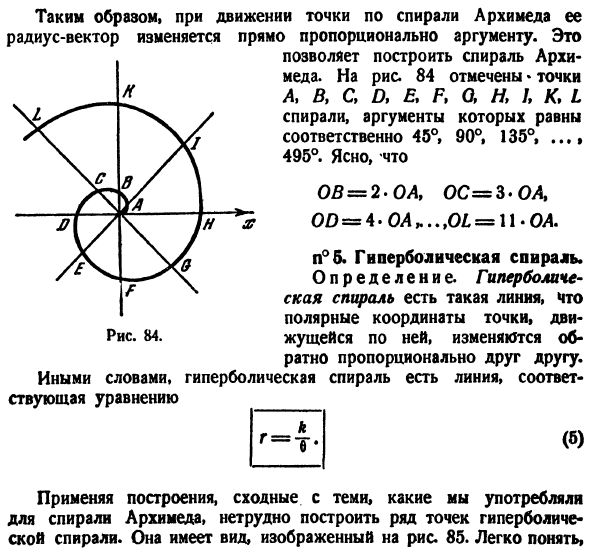
точка движется к спирали аркимеда, ее радиус-вектор изменяется прямо пропорционально argument. It есть Вы можете построить спираль Архимеда. На рисунке 84 отмечены * точки AAC, d, аао, я, я,/, Hell спирали. Аргументы равны 45°, 90° и 135° соответственно…«Равняется 495°. это понятно 05 = 2. ОА, ОС = = З. ОД ОД = 4 * ол…, 01 = 11 * ОА. П°5.Гиперболическая спираль.
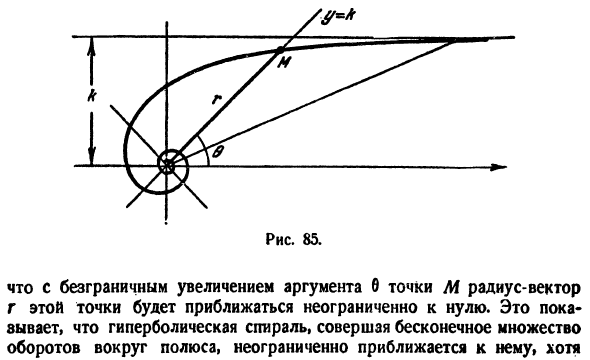
Определение гиперболической спирали означает, что полярные координаты точки равны 84.Пережевывая его, они меняются, наоборот, друг на друга. То есть, гиперболическая спираль-это линия, соответствующая выражению. (б) Нетрудно построить множество точек гиперболической спирали, используя структуру, подобную той, что использовалась для Архимеда Helix. It имеет форму, показанную
на рисунке. 85.Легкий для понимания Рисунок 85. Если точка M аргумента b увеличивается бесконечно, радиус-вектор r в этой точке приближается к неограниченному нулю. Это указывает на то, что гиперболическая спираль, которая бесконечно вращается вокруг полюсов, приближается к бесконечности, но、 Никогда не достигать. Эта ситуация выражается в том, что полюса служат
асимптотическими точками гиперболической спирали. Чтобы установить еще одно свойство гиперболической спирали, мы также вводим декартову систему координат, в которой начало координат совпадает с полюсами, а горизонтальная ось совпадает с poles. As вы знаете, для любой точки M (r, b)= M (x, y) х = р COS в б,^ =
rsin6.Поэтому для точек, находящихся на спирали (5)、 Преступление 9 / / > v г = К-и J -. (6) В следующей главе, по мере приближения О.、 Когда он достигает нуля, отношение равно 1.Но、 Когда он достигает нуля, согласно (5), точки М (р, б) будет бесконечно спираль(потому что бесконечно R увеличивается).Таким образом, из (6), ордината у точки М, которая уходит в бесконечность вдоль гиперболической
спирали, стремится быть число k. Так что прямой у = к выступает в качестве асимптоты спираль(5). Н * 6.It-это Рембрандт. как указано в n # 5, я счел удобным использовать 2 системы координат полярных и прямоугольных координат для изучения гиперболической спирали. То же самое верно, если рассмотреть другую интересную кривую-лемнискат -. Определение лемниската-это линия, представляющая геометрическое положение точки, а произведение расстояния
от 2 заданных точек (фокусов) является постоянной величиной, равной 2-кратному фокусному расстоянию. Уравнение лемниската выводится в прямоугольной системе координат, где ось абсцисс проходит через фокальную точку, а начальная точка делит пополам сегменты между фокальными точками. Если обозначить фокус лемниската через F и F, а FF = 2c, то указанная система координат
имеет F (ct 0) и F (- су0).так, для любой точки M(x, y)、 МФ = г (х-с) 9 + м, МЖ = г (х + с) 9 + у9、 И уравнение ремниската Г (х-с) 9 — \ — уу * у(Х + с) * + у ’= д *. Мы упростим это уравнение, возведя его в квадрат. Или то же самое СХ * + у9 + с)- 2СХ] с «4 — С9)+ 2СХ] = с*. Отсюда (х 9 + у9 + С9) 9-4s9x * = з * Или (Х9 — \ — г * г + 2С9(Х1 + г’) — Джей-С4 — * в = СКзнак+ C. наконец, из(2) Для краткости, если вы установите 2c * = a1,
вы найдете окончательное уравнение лемниската. младший»+ /)•» «■<*•-Л Итак, это кривая 4-го порядка. Уравнение (7) содержит x и y только в четных градусах, поэтому соответствующая кривая симметрична на обеих осях. Поэтому, чтобы установить форму ремниската, достаточно найти форму его части в первом координатном угле. Для решения последней задачи введем полярную
систему координат с осью Ox в качестве полярной оси и координатой Ox в качестве полюсов. И затем… x-r cos 0, y-t sin 0 и выражение (7) принимают следующий вид: Или•) (8) ] икс Рис.87. Р * 〜А * Р *(потому что б-sin16) Р * = А * соѕ 20. Из этой формулы ясно, что если 6 = 0, то получается r = a. когда in начинает
увеличиваться от 0 = 0 до 0= -^ -, r уменьшается от r = a до r = 0.Однако значение 0 равно、 П 1С числа между x и * 2 (7 )) икс Рис.86. в мнимом значении r нет точки, то есть остатка от указанного 0**.Итак, как показано на рисунке 1, в части лемниската в 1-м координатном углу имеется рейка. 86, и весь лемнискат, как показано на рисунке 87. * ) вы можете уменьшить уравнение с помощью
r1.Правда, такое снижение может привести к потере точек r = 0, но этого не произойдет. Точка на кривой (8) соответствует значению^0 = — j. •Затем r — * 0, то есть сделать точку M(r, b) ближе к полюсам. Она сама по себе является остатком. Луч ом (образующий ось полюса и угол 6) оказался секущим ремникато. Если эта фекция стремится соответствовать биссектрисе y = x первого угла. Поэтому лемнискат начала отсылает к биссектрисе.
Смотрите также:
| Преобразование координат | Переменные и их пределы |
| Упрощение уравнений кривых 2-го порядка | Функция |

