Оглавление:



Полуэмпирические выражения для турбулентного массового потока
- Турбулентный массовый поток, возникающий в уравнении (19.9), должен быть выражен СА или градиентом концентрации. Когда с потоком импульса и энергии, определяемым пульсацией турбулентности, существует несколько эмпирических представлений массового потока турбулентности. Все они аналогичны формуле, приведенной в разделе 12.3, поэтому они ограничиваются немного более простой нотацией. Этот поток. Вихревая диффузия*.
Различные результаты показывают значительное расхождение, так что требуется дополнительная работа, чтобы выяснить процесс переноса тепла при пленочном охлаждении. Людмила Фирмаль
По аналогии с законом диффузии Фика напишите следующее уравнение: (19.10) RDV-коэффициент диффузии турбулентности или коэффициент диффузии вихря. Из-за сходства теплопередачи и массопереноса часто предполагается, что P ^ w /a’1 = 1.Где a1-коэффициент термодиффузии вихря. Некоторые исследователи считают, что соотношение= 0,5 + 1(см. раздел) 12.3). Формула для длины смешанного пути Прандтля и Тейлора.
- Подобно уравнению (12.10), найдите следующее: (19.11). Где I-длина пути смешения и обычно принимается равной потоку в канале, а y-расстояние от стенки. Представление на основе портрета кармана hypothesis. By аналогия с уравнением (12.11)、 А * * * | (д ^ / д ^ ч диджей、 (19.12) Где x₂-та же константа, что и в формулах (5.16) и (12.11). Опыт теменной Deissler.
Это означает, что решение уравнения энергии может быть получено путем наложения двух решений, одно из которых учитывает сосредоточенные стоки тепла только как пограничное условие, в то время как другое решение получено для распределенных источников или стоков. Людмила Фирмаль
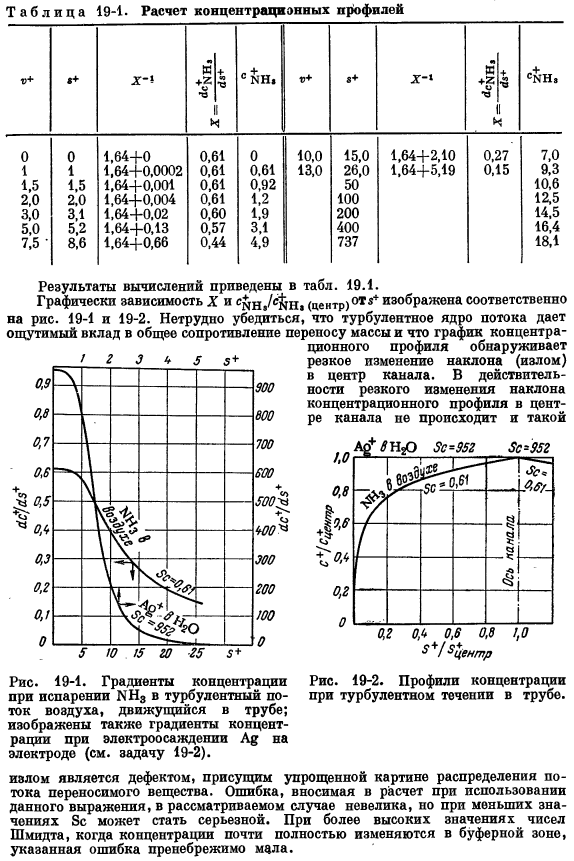
Аналогично уравнению (12.12), Дайслер предложил следующую формулу: 111-п * * п(= + = ^)] ^-( «ха Где величина n совпадает с формулами(5.17) и(12.12). Уравнение (5.31), Sc-Прантл. Запись прп е Sxd> ’ С 1.64 + 0.0154 г * 1> * [1-ехр (-0.0154 с * я*) Дж (0 = СС * = Раздел 26) ’(19.17) c£Hₜ= 9.3 + 2.781 n — ^ r =-0.3 +2.781 пз * (26 s * ss 737) (19.18) Воздушный поток Razvod / RazvodS может графически отображать профиль плотности колонны. 。Для доказательства И1.
Смотрите также:

