Оглавление:
Положение центра тяжести некоторых однородных тел простейшей формы
Центр тяжести площади треугольника
Разобьем площадь 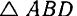 (рис. 90) прямыми, параллельными основанию
(рис. 90) прямыми, параллельными основанию  , на очень большое число очень узких полосок, которые можно рассматривать как отрезки прямой линии. Центр тяжести каждого отрезка лежит в его середине. Отсюда заключаем, что центр тяжести треугольника лежит где-то на линии, соединяющей середины этих отрезков, т. е. на медиане
, на очень большое число очень узких полосок, которые можно рассматривать как отрезки прямой линии. Центр тяжести каждого отрезка лежит в его середине. Отсюда заключаем, что центр тяжести треугольника лежит где-то на линии, соединяющей середины этих отрезков, т. е. на медиане 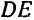
 .
.
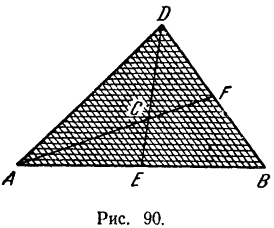
Разбив площадь треугольника прямыми, параллельными какой-нибудь другой стороне, например  , и рассуждая аналогичным образом, мы придем к тому, что центр тяжести площади треугольника должен лежать на медиане
, и рассуждая аналогичным образом, мы придем к тому, что центр тяжести площади треугольника должен лежать на медиане  . Следовательно, он лежит в точке пересечения медиан треугольника.
. Следовательно, он лежит в точке пересечения медиан треугольника.
Так как точка пересечения медиан треугольника делит каждую из них в отношении 1:2, то центр тяжести площади треугольника находится на его медиане на расстоянии одной трети медианы от точки пересечения медианы с соответствующей стороной треугольника.
Для определения центра тяжести площади произвольного многоугольника разбиваем его на треугольники и определяем их центры тяжести. Считая вес каждого треугольника приложенным в его центре тяжести, находим теперь центр системы полученных таким путем параллельных сил.
Центр тяжести дуги окружности
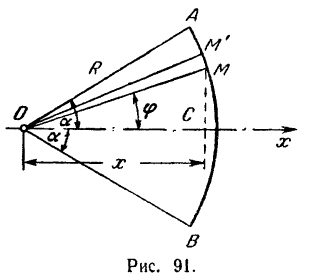
Пусть дана дуга 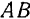 окружности радиуса
окружности радиуса 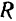 с центральным углом
с центральным углом 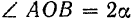 (рис. 91).
(рис. 91).
Возьмем начало координат в центре 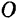 окружности и направим ось
окружности и направим ось 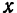 по биссектрисе центрального угла. Так как эта ось является осью симметрии дуги, то центр тяжести дуги лежит в какой-то точке
по биссектрисе центрального угла. Так как эта ось является осью симметрии дуги, то центр тяжести дуги лежит в какой-то точке 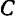 этой осн. Следовательно, ее положение вполне определяется одной координатой
этой осн. Следовательно, ее положение вполне определяется одной координатой 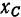 .
.
Разобьем дугу 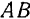 на отдельные элементы. Координата центра тяжести однородной линии определяется по формуле (47)
на отдельные элементы. Координата центра тяжести однородной линии определяется по формуле (47)
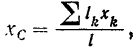
где 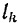 — длина одного элемента линии,
— длина одного элемента линии, 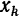 — координата центра тяжести этого элемента.
— координата центра тяжести этого элемента.
Будем неограниченно увеличивать число элементов, на которые мы разбиваем дугу  , стягивая их в точки, и перейдем к пределу. Тогда числитель формулы (47) обратится в определенный интеграл, распространенный на всю длину дуги, и мы получим формулу:
, стягивая их в точки, и перейдем к пределу. Тогда числитель формулы (47) обратится в определенный интеграл, распространенный на всю длину дуги, и мы получим формулу:
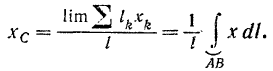
При достаточном уменьшении элемента 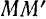 дуги
дуги 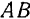 можно считать, что точки
можно считать, что точки 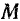 и
и 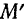 сколь угодно близко отстоят друг от друга и потому положение элемента
сколь угодно близко отстоят друг от друга и потому положение элемента 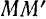 (рис. 91) определяется углом
(рис. 91) определяется углом 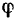 , координата его центра тяжести
, координата его центра тяжести 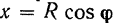 и длина элемента
и длина элемента 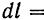
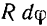 .
.
Подставляя значения 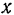 и
и 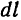 в подынтегральное выражение, будем иметь
в подынтегральное выражение, будем иметь
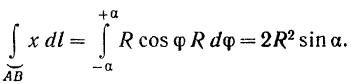
Длина же дуги 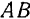 будет, очевидно, равна
будет, очевидно, равна 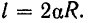
Отсюда по формуле (47а) получаем:
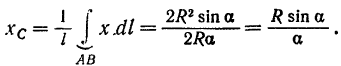
Следовательно, центр тяжести дуги окружности лежит на ее оси симметрии и отстоит от центра окружности на расстоянии, равном
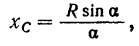
где 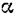 — половина центрального угла в радианах.
— половина центрального угла в радианах.
Центр тяжести площади кругового сектора
Пусть дан круговой сектор 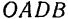 радиуса
радиуса 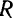 с центральным утлом
с центральным утлом 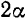 (рис. 92). Примем за начало координат центр
(рис. 92). Примем за начало координат центр 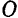 круга и направим ось
круга и направим ось 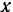 по радиусу
по радиусу 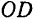 , проведенному через середину дуги
, проведенному через середину дуги 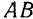 . Разобьем данный сектор на
. Разобьем данный сектор на 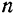 равных элементарных секторов. В пределе, при неограниченном увеличении числа секторов, последние можно рассматривать как равнобедренные треугольники, центры тяжести которых лежат на дуге окружности радиуса
равных элементарных секторов. В пределе, при неограниченном увеличении числа секторов, последние можно рассматривать как равнобедренные треугольники, центры тяжести которых лежат на дуге окружности радиуса 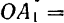
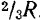 . Силы тяжести всех элементарных секторов равны между собой вследствие равенства их площадей. Задача, таким образом, сводится к определению центра равных параллельных сил, точки приложения которых равномерно распределены по дуге окружности
. Силы тяжести всех элементарных секторов равны между собой вследствие равенства их площадей. Задача, таким образом, сводится к определению центра равных параллельных сил, точки приложения которых равномерно распределены по дуге окружности 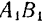 т. е. в пределе при неограниченном увеличении числа
т. е. в пределе при неограниченном увеличении числа 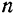 элементарных секторов, к определению центра тяжести однородной дуги
элементарных секторов, к определению центра тяжести однородной дуги 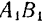 .
.
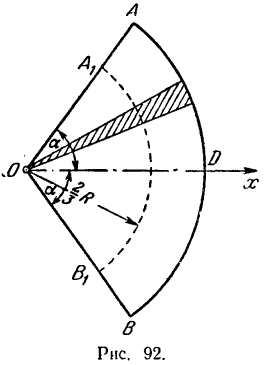
Подставляя значения радиуса дуги 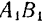 в формулу (48), находим, что центр тяжести площади кругового сектора лежит на его оси симметрии и отстоит от центра круга на расстоянии, равном
в формулу (48), находим, что центр тяжести площади кругового сектора лежит на его оси симметрии и отстоит от центра круга на расстоянии, равном
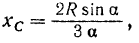
где 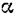 — половина центрального угла в радианах.
— половина центрального угла в радианах.
Формулы для определения положения центра тяжести целого ряда других геометрических тел можно найти в различных технических справочниках.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

