Оглавление:






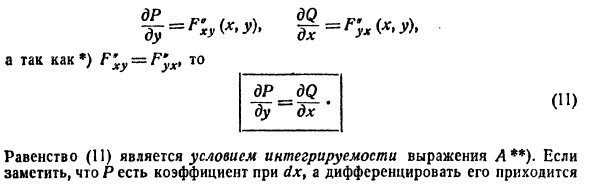
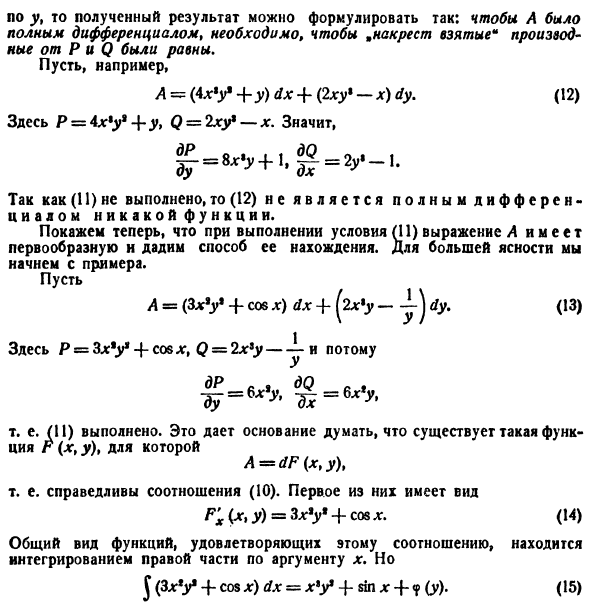


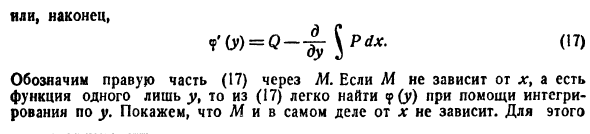


Полный дифференциал
- Полный дифференциал № 1. Определение дифференциации. Пусть функция z = f (x, y) имеет непрерывную производную по x и y. Измените точку (x, y) и дайте bx и ay в качестве аргументов. Как видно из §1, соответствующий прирост Az можно выразить в следующем виде: Ar = Br (x, Y) b * + fy y) b y + b 0) Где p = Y (bx)% — f- (by) \ lim e = 0, а f’x и fy рассчитываются точно Р-д Я исправил это в тот момент (х, у). Если p — ►0, произведение ep имеет бесконечно меньший порядок, чем p.
AU) b * + Gu (*> y) by- (2) Правая часть этого выражения называется полной производной функции z = f (xt y) и выражается через dz и df (x, y). так df (x, y) = fx (x, y) bx + fy (x, y) b (3) (4) Или, короче говоря, dz = z’x Ajc -f- z’y by. Уравнение (2) fo ^ dz, То есть приращение функции приблизительно равно разности *), и чем выше точность этого уравнения, тем меньше приращение аргумента. Пример. Дай мне z = 2jfiy + 3xy + l (5)
Поэтому для очень маленьких Ad: и Au этот продукт часто можно игнорировать, что приводит к приближению. Людмила Фирмаль
Отсюда? ‘(Y) = -y и это началось, <p (y) = -In ^ -C *). в конце концов F (xt y) = x * y * + sin dg-1n.y + C. Метод фактического создания функции F (x, y) имеет один недостаток. Место, где использовалось условие (11), неясно. Чтобы понять это, примените тот же метод к уравнению (12). (12) не является полной разницей в функции, поэтому ясно, что препятствия, которые не могут быть преодолены, должны встретиться где-то на нашем пути.
Как и для (13), (12) также ищем общий вид функции F (x, y). F’x (xty) = P (xty) = 4x * y * + y Эти функции заключаются в следующем: F (*, y) = J (4x * y * + y) dx = xy + xy + 9 (y). Встретить отношения F’y (x, y) = [xy + xy + h (y) i; = 2xu8- *, вам нужно выбрать <p (y), как оказалось 2x4y 4-x + y ‘(y) = 2 xy * -x или <? ‘(Y) = 2xu% -2x * y-2x, Это явно невозможно, поскольку производная <p ‘(y) не может зависеть от x.
Так что здесь есть нарушение условия целостности! Теперь рассмотрим вопрос в общем виде. Дай мне A = P (x, y) dx + Q (xly) dy, (16) Кроме того, (11) выполнено. Общий вид функции F (x, y) F’x (x, y) = P (x, y), Это **): F (xty) = $ P (xiy) dx + <t (y) t Где <p (y) — совершенно произвольная функция от y. Для F’y = Q вам нужно выбрать <p (y), чтобы получилось Или у $ РЛг + * ‘(у) = Л
- Или наконец ? ‘O>) = 0 — ^ \ Pdx. (17) Правая часть (17) представлена М. Если не не зависит от x и является функцией только y, легко найти <p (y) из (17) путем интегрирования по y. Ми указывает, что на самом деле это не зависит от х. Для этого Достаточно проверить это но дх ~ дх дх (ду) да \ * д * Используя тот факт, что нет x при расчете порядка дифференцирования Не против Поведение дифференцирования и интеграции для одной и той же переменной противоположны. смысл 4 $ <■ «- <■ • так йМ дх дх ду • Учитывая (II), это означает (18).
Другими словами, вы можете найти требуемое <p (y). Итак, мы доказали Теорема (16) является полной производной, только если выполнено (11). Кроме того, при выполнении (I) существует способ фактически построить обратную производную (16). Замечания. Для одной переменной полное семейство (16) антипроизводных имеет вид F (x, y) + C, (19) Где F (x, y) является одним из этих антипроизводных, а C является константой.
Это означает, что R (q, y) не изменяется с x, не изменяется с y, то есть не изменяется вообще. Следовательно, y) = c, то есть Fx (x, y) -F (x, y) = C и Fx (x, y) можно выразить в виде (19).
Фактически, если Ft (x, y) является другим примитивом, чем F (x, y), разница между R (.x, y) = Ft (x} y) -F (x, y) будет равна нулю в противном случае То есть Rx = Ry ~ 0. Людмила Фирмаль
Если заданы значения x и y на основе значений x = 2, y = 1, приращения Ajc = 0,01 и Au = 0,02, найдите значения Az и dz. Значения x = 2, ^ = 1 соответствуют 2 = 15. Новые значения для x-f-f-Ax = 2.01 и .y = 1.02 соответствуют z-j-Az = 15.392404. смысл A * = 0,392404. *) Сумма производных зависит от точек производной (x, y) и приращений Lx и Dy. В (5) вычисляется разница dz между этими x и y, на основе которой аргументы получают приращения D * и Dy, что вызывает Dg, который должен быть заменен этими значениями Ад: Dy нет.
С другой стороны, gx = 4xu + 3y, z’y = 2x% bx. Если g2 = 2 и y = 1, то gx = 11 и zy = 14. Таким образом, dz = 11 • 0,01 + 14 • 0,02 = 0,39. Следовательно, абсолютная ошибка уравнения Az ^ dz составляет 0,002404 и относительная 0,002404 0,003 _ n n fl / 0,392404 ^ 0,3 ‘/ г Полная производная функции любого числа аргументов определяется аналогично. Например, если u = f (x, y, r) rftt = u ^ bx -f-uy by -f-u’z Здесь небольшая инкрементная производная аргумента почти идентична функции инкремента.
Давайте посмотрим на некоторые примеры. 1) Пусть z = x * y%. Найти dz с x = > V = 2 и Ax = Au = 0.3. Где zx = bx * uch = 12, Zy = 2x3u = 4. Поэтому y, Axe, Du dz. Где dz = yx? ~ X по Ax — \ — xy \ nx. 4) d (x * ztzigy) = 3x * zxztgy Axe + • 5) dex 8.0 y = e * h, ny sin y Ax + f * eln * jc cos j / Dy. Интересным примером является функция z = .v. Где zi = l, zj, = 0, поэтому dz = Ax, т.е. дх = д *. Точно так же dy = Ay. Другими словами, разница аргументов соответствует приращению. Вернитесь к Уравнению (3) и замените Ад в нем. Получи Dy от Au.
df (x, y) = f’x (x, y) dx — \ — fy (x, y) dy. (6) Различия обычно пишутся в этом формате. В заключение, требование экстремального значения функции z = f (x, y), состоящей из уравнений f’x (x, y) = 0, f’y (x, y) = 0, равно одному Обратите внимание, что это может быть записано как выражение. (7) df (x, y) = 0
Фактически, если вы применяете Dx и Au, если вы берете u (7) Ax = 1, Dy = 0, вы найдете f * (x, y) = 0. Аналогично, из (7) в f’y (x, y) = 0. № 2. Использование дифференцирования в теории ошибок. Предположим, что величина z = f (x, y) зависит от x и y и интересуется значением Zq, соответствующим системе со значением x = x <> y = y0.
Для каждого измерения значение измеренной величины является только приблизительным, и ошибка неизвестна, но только число знает, что ошибка не может быть превышена. Это число (.limit error *) зависит от точности используемого оборудования. Например, если конкретный объект взвешивается по шкале, обеспечивающей точность в 1 мг, а показание 323 мг берется по шкале * веса, то можно гарантировать только то, что истинный вес объекта составляет от 322 до 324 мг. Я не могу Где 1 мг — предельная ошибка.
Знание предельной ошибки измеренного значения x0 и определение предельной ошибки zo, которая больше не измеряется напрямую, вызывает естественные вопросы. Это рассчитывается из измеренных х0 и у0. Дифференциальная теория дает решение этой проблемы. Конечно, измеренные значения не являются x0 и x0 — [- Dx и + — {- D ^, где | a- | и | do- | не превышают соответствующих предельных ошибок lx и ay. Однако при расчете не z0 = f (x0l y0), а z0 + Az = / (x0-f-Dx,. Y0 + Dy) -разница Az может быть заменена дифференциалом dz *. Итак, ошибка Az dz = fx (x * yo) Ax + fy (Ho, Yo) Au, удовлетворяет неравенству ) A * KI / I ( + Yo) IV (8) Пример.
Измерения на сторонах прямоугольника составляют x = 5 м, y = b m, предельная погрешность измерения длины составляет 0,5 см, а площадь прямоугольника составляет z = xy = 15 мг. Ошибка в этом значении из-за (8) оценивается следующим образом: I | <en, -f-hou = (3 • 0,005 -f-5 • 0,005) мг = 0,04 м \
Уравнение (8) может быть использовано для установления ряда правил, используемых в теории ошибок. Я объясню два из них. I. Если z = x -} — y, dz = Ax-J-Du, почему | AZ | II. Когда z = xy, делим на dz = yAx + xAy и | | >> | ax-f- | A-joy \ z \ = \ xy \ DG Z Oh Oh \ X \ 1 | ил То есть критическая относительная погрешность продукта равна сумме критических относительных погрешностей факторов. n ‘3. Полностью дифференциальная интеграция. формула dF (x: y) = Fx (x, y) dx + Fy (x, y) dy (6)
Указывает, что существует формат полной разницы P (dg, y) dx + Q (x, y) dyt Где P (g, y) и Q (x, y) являются функциями от x и y. Например, если F (xfy) = Зл: У + 2л- dF (x, y) — (6x + 2) dx + bx * y dy, То есть здесь P = 6xu * + 2, Q = bxly. Для многих задач (например, динамика точек) важно уметь решать следующие задачи: спросил я. Данное выражение A = P (xt y) dx + Q (x, y) dy. Узнайте, является ли A полной производной функции, и если да, найдите эту функцию (называемую обратной производной A).
Пожалуйста, обратите внимание на отношения A = dF (x, y) (9) Эквивалент двум связанным системам Py) = F’x (.x, y), Q (x, y) = F ′ / x, y). (10) Если эти отношения выполнены,Уравнение (11) является условием интегрируемости уравнения A **). Если вы заметили, что P является коэффициентом dx, и вам нужно дифференцировать его д-р дк Сделать (Р) И *) F’xy = F’yx, ш
Для y мы можем сформулировать результат следующим образом: Чтобы А бился с полным дифференцированием, «производные» производные от Р и Q должны быть равны. A ~ (4xU + y) dx + (2xu * -x) dy. (12) Где P = 4xY + yt Q = z 2xu * -x. смысл (12) не является полной производной функции, потому что (11) не выполняется. При условии П1) мы покажем, что выражение A имеет примитив и как его найти. Давайте начнем с примера для ясности.
Дай мне A = (3 * Y-f cos x) dx-f (bc% y-y j dy. (13) Где P = 3xY 4-соевый q, Q = 2x’y- отсюда DR dQ s То есть (11) выполнено. Это дает основание полагать, что функция r (q, y) существует. A = dF (дг, у), То есть соотношение (10) является действительным. Их первая форма R’zh (dg, y) = 3x * y * + soe x. (14) Общую форму функции, которая удовлетворяет этому соотношению, можно найти, интегрируя правую часть относительно аргумента q. но $ (3 * Y + cos x) dx = * Y + sin l: -f <p (y). (15)
Дело в том, что когда задействована функция одной переменной, чтобы получить полное семейство антипроизводных, возьмите одну из них и добавьте к ней произвольную постоянную C, то есть величину, производная которой равна нулю Обратите внимание на. То же самое сделано здесь, но величина, что производная по x равна нулю, может зависеть от y. Поэтому в правой части (15) вместо C. записывается функция
Y) = [xV + smx + <t (y) Yy = 2x * y-l-милли, это то же самое, 2x * y + h ‘(y) = 1x * y- •
Смотрите также:
| Производные функции нескольких переменных | Понятие о системах дифференциальных уравнений |
| Экстремальные значения функции нескольких переменных | Двойной интеграл |

