Оглавление:




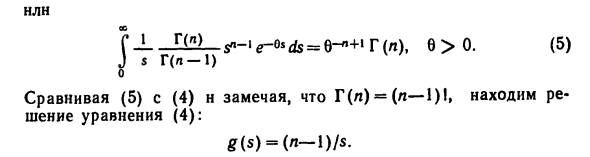

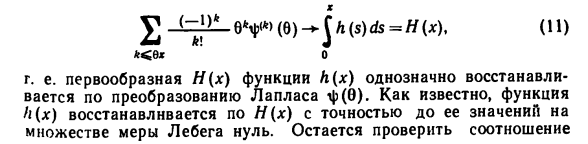

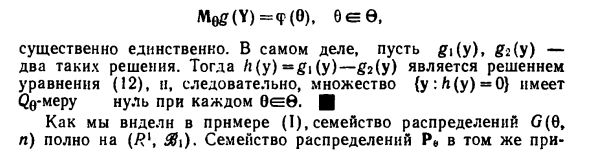

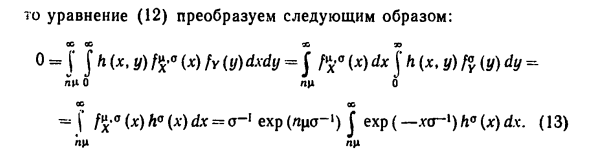

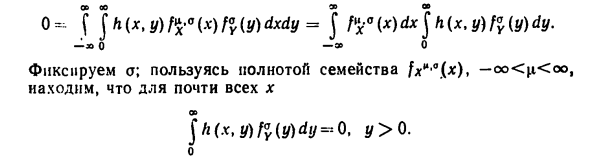


Полные достаточные статистики
- Рассмотрим уже готовую статистическую модель (SB, 31, {&}) Познакомились с различными примерами числовых функций Функция неизвестного распределения вероятности ), где любая точка t считается максимально возможной Неизвестное значение «r (c) (f (P)). termh.’o.yup:; Выполнить задачу Оценка очков, мы должны рассмотреть различные статистические данные 7 «(x) возможные оценки 0; t = l p), I-II„ ППп +, Family Re, 8> 0, можно выразить как / 0 (xn) = exp (-8 2 x,), x „e = R» +, Случайная выборка Xn = (Xi, …, Xn) Я ел самостоятельно. с. Плотность распределения 8e ~ vdg, dc> 0 соответственно. ДОС N Точная статистика: S (xn) =? , Vi.
C) Уравнение Б) принимает форму (N), 6> 0. D) Если g (s) является решением D), изменить произвольно Изображение на множестве нулевых мер Лебега, найти решение снова Уравнение D). До этого вида Неоднозначность, уравнение D) имеет единственное решение, Не сложно найти. На самом деле, C) заменить n на n-1 Мы пишем NLN OS Я -T (n) s «-‘e — ** ds = 6- * +» T (s), 6> 0. E) s G (n-1) E) и D), и Γ (n) = (n-1I, Решение уравнения D):
Напишите формулу А) (Если р (8) = 8: j = eI e> o B> S (X ,,) имеет плотное распределение G (8, n) (см. р. 1, 2§7) B ^ ** S> ° Людмила Фирмаль
Думай как уравнение для А3) Исправлено, это легко увидеть, за исключением набора мер Ноль Лебега, ха (х) = 0, и, следовательно, почти все х и Я A4) Используйте полноту семейства G (cr ‘, n-1), чтобы получить H (x, y) = 0. для | Почти все y) всех x, для которых выполняется A4, и N Докажите целостность статистики (nx (i), Y \ (xA) -a-A))). 1 = 2 (IV) Модель повторной выборки из распределения A ‘(q, a2) n «_ Статистика завершена (Y] A * «> Y] (* i-x) d) -check Во-первых, распределение ((μ, оо) ua (β ‘, 3 & ), где — оо <μ < <-foo, ao2> 0-Модифицировано, завершено.
Для того, чтобы использовать Это двустороннее преобразование Лапласа ФF) = f e-exg (x) dx, -oo <6 <+ oo, A5) -00 Определить функцию g (x) однозначно для почти всех x. Формула А2) Семейство N после элементарной (μ, o02) Преобразование принимает форму оооо Это сокращается до A5 путем замены переменной y = xjoo2. A (x) = 0 почти везде. н н X = YX «Y» = E (* «- ^) * -X и Y независимы, Прокладка и распределение N (n \ i, a2) и G (l / Ba2), (n-1) / 2), то пара статистики в уравнении A2) P | P _ V x, -, V (* i-jcJJ является я = я 1 = 1 O = -? ] h (x, y) fy (x) / «(y) dxdy = j / ^» (jf) dxjЛ (x, y) / «(y) dy. 0 О ] -0
- Исправить; используя полноту семейства ^ x «| 0. (x), -oo <η <oo, Почти для всех х о 158 CA / Ba2), в настоящее время используется целостность семьи (n-1) / 2) (см. Пример (I)), для почти всех y и почти всех x, Cx, y) -0. W Следующее сделано Теорема 1. Пусть плотность fe (x) принадлежит параметру k Экспоненциальная семья: f (x) = h (x) exp (j \ at (c) Γ, (x) + b (c)). е = 0 1 = 1 Набор значений функций a (b) = (a \ (b), …, ab (b)), Поскольку k-мерный параллелепипед включен, T (x) = (Γ, (x), …, , .., 7 «* (x)) — Достаточно полная статистика.
Доказательство теоремы можно найти в [11, 12]. Людмила Фирмаль
Смотрите также:
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.

