Оглавление:
Полное исследование функций и построение графиков
Под полным исследованием функции понимается решение следующих вопросов:
1) определение области существования функции;
2) выяснение вопроса о чётности, нечётности, периодичности функции;
3) определение точек разрыва. Определить точки пересечения кривой с осями координат (если они существуют);
4) определение асимптот графика функции;
5) определение интервалов возрастания и убывания функции, определение экстремума функции;
6) определение интервалов выпуклости и вогнутости графика функции, определение точек перегиба;
7) произвести необходимые дополнительные вычисления;
8) построить график функции.
Задача №66.
Исследовать функцию 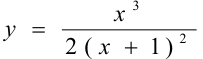 .
.
Решение:
1. Определим область существования этой функции. Функция существует для любых 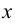 , кроме
, кроме 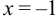 , при которых знаменатель дроби обращается в 0. Значит, функция определена в интервалах
, при которых знаменатель дроби обращается в 0. Значит, функция определена в интервалах 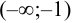 и
и 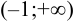 .
.
2. Исследуем вопрос о чётности или нечётности функции. Проверим для этого выполнение равенств 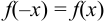 и
и 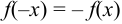 .
.
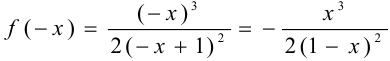 , т. е. ни одно из этих равенств не выполняется, значит, функция не является чётной и нечётной. Функция также не имеет периода.
, т. е. ни одно из этих равенств не выполняется, значит, функция не является чётной и нечётной. Функция также не имеет периода.
3. Определим точки разрыва, если они существуют. Числитель и знаменатель дроби 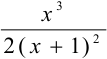 непрерывные функции, поэтому функция
непрерывные функции, поэтому функция 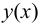 будет непрерывной при всех значениях
будет непрерывной при всех значениях 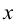 , кроме
, кроме 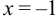 , при которых знаменатель дроби равен 0.
, при которых знаменатель дроби равен 0.
График функции будет пересекаться с осями координат в точке с координатами (0; 0), так как при 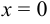
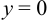 .
.
4. Определим асимптоты графика:
а) вертикальные асимптоты найдём, приравняв знаменатель к 0. 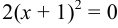 ,
, 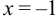 , т. е. уравнение вертикальной асимптоты
, т. е. уравнение вертикальной асимптоты 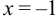 ;
;
б) найдём горизонтальные асимптоты.
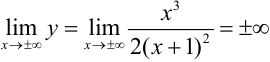 , т. е. горизонтальных асимптот нет;
, т. е. горизонтальных асимптот нет;
в) наклонные асимптоты:
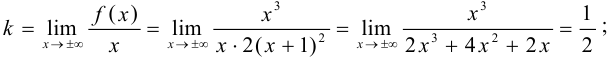
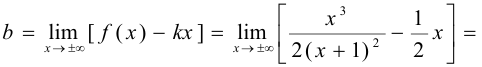
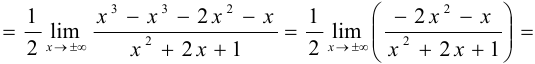
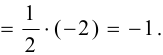
Наклонная асимптота одна: 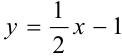 .
.
5. Определяем интервалы возрастания и убывания функции и экстремум функции. Для этого найдём первую производную:
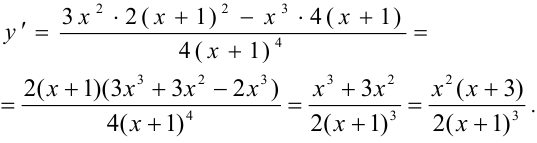
Определим критические точки. Решаем уравнение 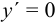 .
. 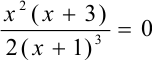 или
или 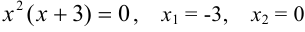 .
.
В точке 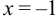 функция неопределена. Эти точки разделяют интервал существования функции на такие интервалы:
функция неопределена. Эти точки разделяют интервал существования функции на такие интервалы: 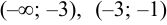 ,
, 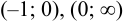 .
.
Рассмотрим, какие знаки принимает первая производная в каждом из этих интервалов.
В интервалах 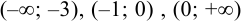 первая производная положительна, а в интервале (-3; -1) первая производная отрицательна.
первая производная положительна, а в интервале (-3; -1) первая производная отрицательна.
В интервале 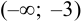 функция возрастает, в интервале (-3;-1) -убывает, в интервалах (-1; 0) и
функция возрастает, в интервале (-3;-1) -убывает, в интервалах (-1; 0) и 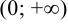 — функция возрастает.
— функция возрастает.
При 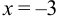 функция имеет максимум, причём
функция имеет максимум, причём 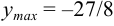 .
.
6. Определим интервалы выпуклости и вогнутости графика функции и точки перегиба. Найдём вторую производную:
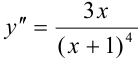 .
.
Определим значениях, при которых 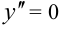 .
.
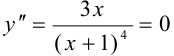 , т.е.
, т.е. 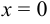 .
.
Критическая точка второго рода 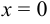 разделяет интервалы существования функции на следующие интервалы:
разделяет интервалы существования функции на следующие интервалы: 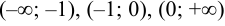 . В каждом из этих интервалов
. В каждом из этих интервалов 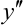 конечна и сохраняет знак.
конечна и сохраняет знак.
Значит в интервалах 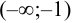 и (-1; 0) кривая выпукла, а в интервале
и (-1; 0) кривая выпукла, а в интервале 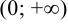 — вогнута. При
— вогнута. При 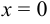 ,
, 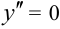 , а при переходе из второго интервала в третий она меняет знак. Это указывает на то, что при
, а при переходе из второго интервала в третий она меняет знак. Это указывает на то, что при 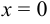 кривая имеет точку перегиба.
кривая имеет точку перегиба.
Построим график этой функции 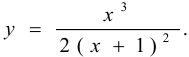
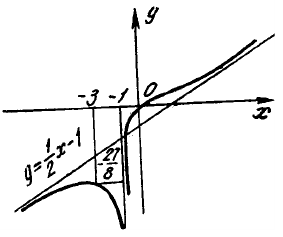
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Точки перегиба в интервале в высшей математике |
| Асимптоты графика функции в высшей математике |
| Функция двух переменных задача с решением |
| Частная производная задача с решением |

