Задача №28.
Полиспаст (механизм для поднятия тяжестей, состоящий из двух систем блоков, каждый из которых смонтирован
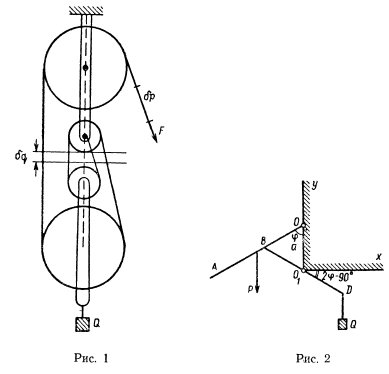
в общей обойме и насажен на отдельные оси, как указано на рис. 1) оснащен нитью, один из концов которой прикреплен к неподвижной точке полиспаста, а другой свободен и находится под воздействием некоторой активной силы  . Нить последовательно обходит как подвижные, так и неподвижные блоки. К нижнему блоку подвешен груз весом
. Нить последовательно обходит как подвижные, так и неподвижные блоки. К нижнему блоку подвешен груз весом  . Определить соотношение величин силы
. Определить соотношение величин силы  и веса
и веса 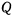 при равновесии системы.
при равновесии системы.
Решение:
Для решения этой задачи воспользуемся принципом возможных перемещений. Пренебрегая горизонтальным возможным перемещением оси симметрии полиспаста, заметим, что система обладает всего одной степенью свободы. Система приводится в движение только тогда, когда перемещается вдоль нити ее свободный конец.
Предположим, что размеры блоков подобраны таким образом, что соответственные части нити, заключенные между обеими системами блоков, можно рассматривать как параллельные. Тогда при перемещении точки приложения силы 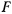 на расстояние
на расстояние 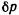 груз поднимается на величину
груз поднимается на величину 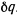 . Общая длина нити при этом остается неизменной и, как видно из чертежа,
. Общая длина нити при этом остается неизменной и, как видно из чертежа,
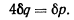
Подсчитывая работу сил на возможном перемещении и приравнивая эту работу нулю, из принципа возможных перемещений будем иметь
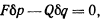
после подстановки значения 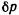 получим
получим
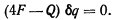
После сокращения на 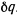 получаем условие равновесия
получаем условие равновесия
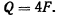
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

