Оглавление:


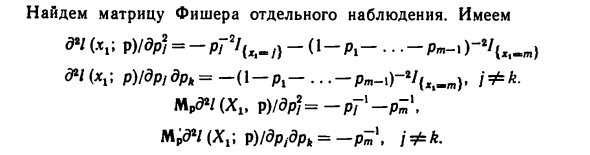




Полиномиальное распределение
- Рассмотрите возможность повторной выборки из распределения, содержащего результаты 1,2, вероятности результата p1, p2, … pt \ P1 + P2 + … + + pm = . Для вектора неизвестных параметров p = = (Pb Pr, · • -, Pm- ). Найди сначала. параметр м.д. IS- Напишите логарифм, используя обозначение индикатора 260 Функция правдоподобия для одного наблюдения: т— \ / ¦ = 1 Где / l = 1, если A истинно, / «= 0, если A неверно. Далее т — 1 n) (xn; P) -? l (jr ‘: p) = S ln p / E 7 (* / = /} ^ L + В «Пи». , , —Pm-l) Y h * ^ ™) » N Xn; P) / 3p, = PT1? /(X.=/)-A-pt-•••-Pm-)~X X Уравнение правдоподобия записывается как
Добавить отношение А7) Подстановка A8) в A7) дает p / n) = vJ «Vn, i = I …, m-1, где v / n) / n указывает непроходную частоту / ‘. / = 1 …, м-1. Для еще. Параметрическая функция mp rt является частотой М результата ВКТЖ / т. Формат статистики H ^ ‘»‘ Найдите матрицу Фишера для каждого наблюдения. У нас есть d * l (x1; p) / dp2l = -pT2Ilxi_l) — (\ — pl -…- pm-i) — d * l (Xl; p) / dp, dpk = — (l-pl -…- Pm_l) -4 {xi_m}, 1 p) / drf = -PTl-Pm \ p p) / dPidPk = -P- \ jφk 261 «1 1 _ 1 1 1 1 … 1 » … 1 … 1 + pTl 0 … o О RT1 … О _ _ _ Рассчитывает статистику W ™. n (v (n »/ n-p) Ixt (P) (v (« Vn-P) » м — 1 / я — 1 (= .1
Первый член справа от A9) т-1 R-! ? Wn) — «ft) i2 = -1 т — 1 1 = 1 / п-1 я = я Мы получаем «P» A9) B0) Людмила Фирмаль
Таким образом, статистика W ^ имеет ограниченное распределение Xm_i Критерий для статистики A9) называется Pearson x2-kiter. Выпишите статистику Wf \ используя A9), B0). n (v («> / n-p) Ixt (v / n) (v (n> / n-p) ‘= м-л -1 (v [n) -np, J1 = Статистические стандарты 1 = 1 V [N] Также называется ссылкой% Пример [5]. При чтении шкалы последняя цифра Числа оцениваются на глаз и часто имеют несколько предпочтений Номер для других. Следующие данные представляют последнюю частоту
Последняя инфраструктура с 200 показаниями по шкале:v / 0 35 1 16 2 15 3 17 4 17 5 19 6 11 7 16 8 30 9 24 Предполагая, что наблюдатель не имеет настроек, Работа с передискретизацией объема l = 200 от полинома Полиномиальное распределение с 10 равными вероятностями результатов: гипотеза Рассчитать статистику числа гипотез A9). V -20 (V / -20) S / 20 15 11,25 -4 0,80 -5 1,25 -3 0,45 -3 0,45 -1 0,05 -9 4,05 -4 0,80 -10 5,00 4 0,80 Результирующие значения 24 и 90. По данным табл. 2.1a [1] для распространения Распределение x2 PR «число 9 степеней свободы использования Вероятность наблюдения того же или Более высокое значение составляет 0,0031.
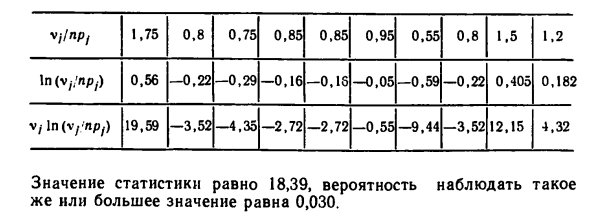
- Это превышает минимум 0,005 минимальный уровень значимости, используемый в статистических таблицах Таблица и гипотеза #o должны быть отклонены. Рассчитать статистику Wf \ по тем же данным У нас есть (V / -20) * 225 16 25 81 16 100 16 Г. 43 1,00 1,66 0,53 0,53 0,05 7,36 1,0 3,33 1,0 Статистика 22,55, вероятность увидеть это Или более высокое значение составляет 0,0074. Для статистики W1 «*, v, 7np / In (Vj / npj) v, -In (\ j’npj) 1 0 19 75 56 59 0 -0 -3 , 8 22 , 52 0 -0 -4 75 29 +0,35 0 -0 -2 85 , 16 0,72 0 -0 -2 85 , 16 0,72 0 -0 -0 95 05 55 0 -0 -9 55 0,59 0,44 0 -0 -3 , 8 +0,22 , 52 1 0 12 0,5 405 +0,15 1 0 4 , 2 182 +0,32
Статистика составляет 18,39, и вероятность наблюдения этого Значение больше или равно 0,030. Людмила Фирмаль
Смотрите также:
| Скалярный параметр | Информация по Шеннону |
| Векторный параметр | Информация по Кульбаку |

