Решение показательных неравенств основано на том, что функция 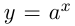 при
при 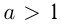 является монотонно возрастающей, а при
является монотонно возрастающей, а при 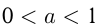 — монотонно убывающей. Отсюда следует:
— монотонно убывающей. Отсюда следует:
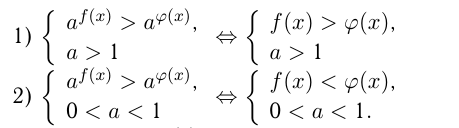
Неравенство 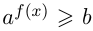 , где
, где 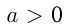 ,
, 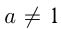 ,
, 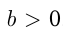 , может быть решено путем логарифмирования обеих его частей, т. к. обе части неравенства положительны. Если
, может быть решено путем логарифмирования обеих его частей, т. к. обе части неравенства положительны. Если 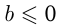 , то неравенство справедливо при всех допустимых значениях
, то неравенство справедливо при всех допустимых значениях 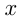 . Неравенство
. Неравенство 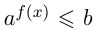 при
при 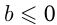 ,
, 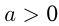 ,
, 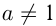 не имеет решений.
не имеет решений.
Простейшие показательные неравенства:
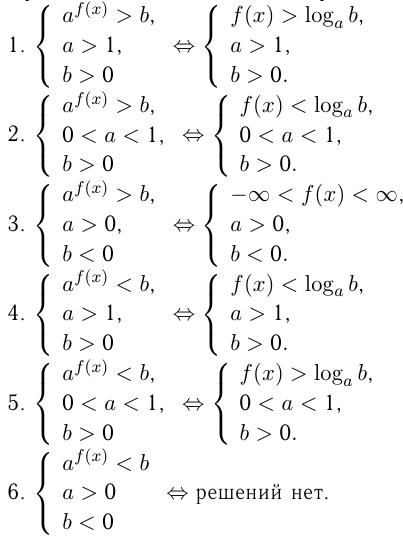
Преобразования показательных неравенств совершаются так же, как и уравнений — путем приведения к одинаковому основанию, методом разложения на множители, путем замены переменных и сведения к рациональному (например квадратичному) неравенству.
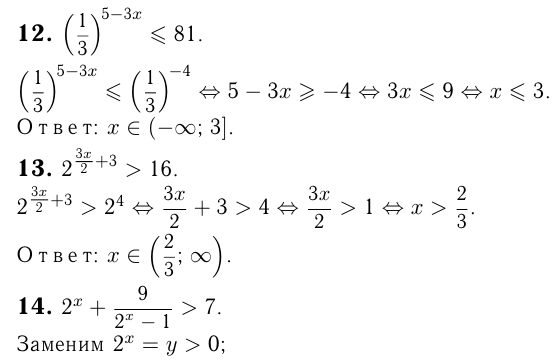

Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач на неравенства |
| Неравенства с радикалами задачи с решением |
| Логарифмические неравенства задачи с решением |
| Тригонометрические неравенства задачи с решением |
