Оглавление:
Показательные неравенства
При решении показательных неравенств используются свойства показательной функции.
Показательная функция 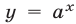 определена на множестве вещественных чисел
определена на множестве вещественных чисел  , является возрастающей при
, является возрастающей при 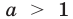 (рис. 23.1) и убывающей при
(рис. 23.1) и убывающей при 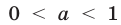 (рис. 23.2), множество значений этой функции — совокупность всех положительных чисел. Неравенства вида
(рис. 23.2), множество значений этой функции — совокупность всех положительных чисел. Неравенства вида
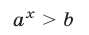
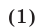
и
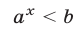
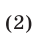
называют простейшими показательными неравенствами.
Если 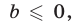 то неравенство (1) является верным при всех
то неравенство (1) является верным при всех 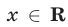 , а неравенство (2) не имеет решений. Пусть
, а неравенство (2) не имеет решений. Пусть 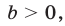 тогда:
тогда:
а) если 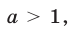 то неравенство (1) справедливо при
то неравенство (1) справедливо при 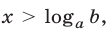 а неравенство (2) — при
а неравенство (2) — при 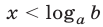 (рис. 23.1);
(рис. 23.1);
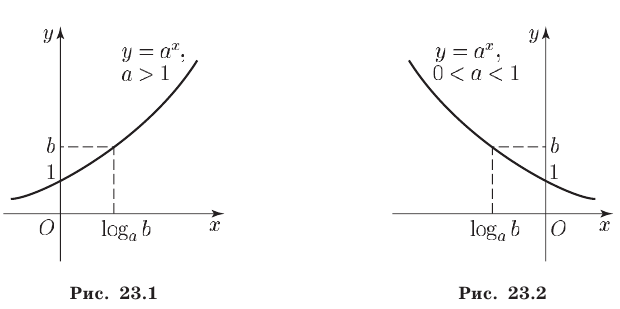
б) если 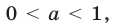 то множество решений неравенства (1) — промежуток
то множество решений неравенства (1) — промежуток 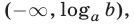 а множество решений неравенства (2) — промежуток
а множество решений неравенства (2) — промежуток 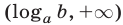 (рис. 23.2).
(рис. 23.2).
Неравенство
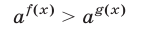
при 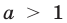 равносильно неравенству
равносильно неравенству 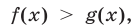 а в случае, когда
а в случае, когда 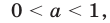 неравенство (3) равносильно неравенству
неравенство (3) равносильно неравенству 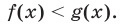
Примеры с решениями
Пример №272.
Решить неравенство 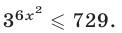
Решение:
Данное неравенство равносильно каждому из следующих неравенств:
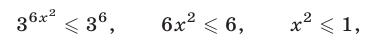
откуда 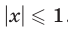
Ответ. 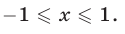 .
.
Пример №273.
Решить неравенство
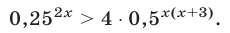
Решение:
Запишем данное неравенство в виде (3), где 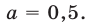 Получим неравенство
Получим неравенство
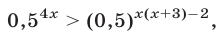
равносильное каждому из следующих неравенств:
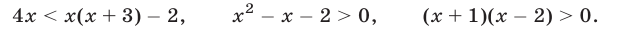
Искомое множество решений — объединение промежутков 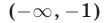 и
и 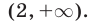
Ответ. 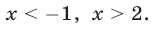
Пример №274.
Решить неравенство
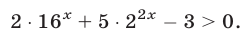
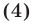
Решение:
Неравенство (4) сведем к квадратному, полагая 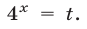 Получим неравенство
Получим неравенство
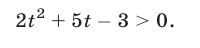
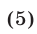
Так как уравнение 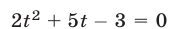 имеет корни
имеет корни 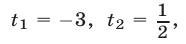 то неравенство (5) можно записать в виде
то неравенство (5) можно записать в виде
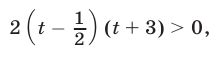
где 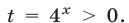 Поэтому неравенство (6) равносильно неравенству
Поэтому неравенство (6) равносильно неравенству 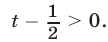 Итак,
Итак, 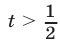 или
или 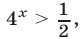 или
или 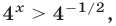 откуда
откуда 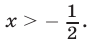
Ответ. 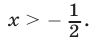
Пример №275.
Решить неравенство
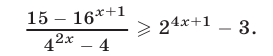
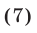
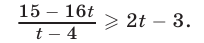
Решение:
Положим 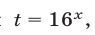 тогда неравенство (7) примет вид
тогда неравенство (7) примет вид
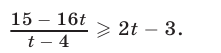

Неравенство (8) равносильно каждому из следующих неравенств :
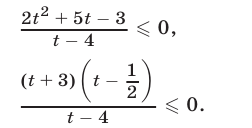

Так как 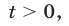 то неравенство (9) равносильно неравенству
то неравенство (9) равносильно неравенству
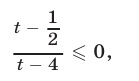
откуда получаем 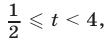 т. е.
т. е. 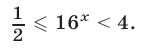
Ответ. 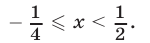
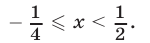
Пример №276.
Решить неравенство
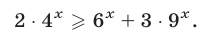
Решение:
Разделив обе части данного неравенства на 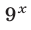 и полагая
и полагая 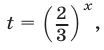 получим неравенство
получим неравенство
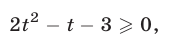
равносильное неравенству
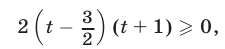
откуда 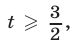 так как
так как 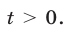 Значит, исходное неравенство равносильно неравенству
Значит, исходное неравенство равносильно неравенству 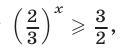 откуда
откуда 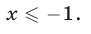
Ответ. 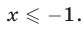
Пример №277.
Решить неравенство
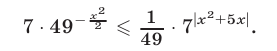
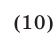
Решение:
Неравенство (10) равносильно каждому из следующих неравенств:
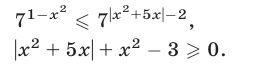
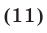
1) Если  или
или 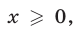 то
то 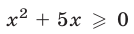 и неравенство (11) равносильно каждому из неравенств
и неравенство (11) равносильно каждому из неравенств
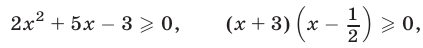
откуда следует, что либо 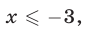 либо
либо 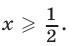 В этом случае решениями неравенства (11) являются все числа
В этом случае решениями неравенства (11) являются все числа 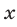 такие, что
такие, что 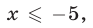 а также все числа
а также все числа 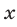 из промежутка
из промежутка
2) Если 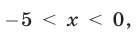 то
то 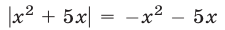 и неравенство (11) примет вид
и неравенство (11) примет вид 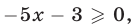 откуда
откуда 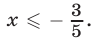 В этом случае множество решений неравенства (11) — промежуток
В этом случае множество решений неравенства (11) — промежуток 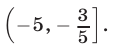
Таким образом, множество всех решений неравенства (10) — объединение промежутков 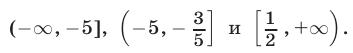
Ответ. 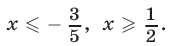
Пример №278.
Для каждого значения параметра а решить неравенство
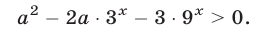
Решение:
При 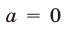 неравенство (12) не имеет решений, так как
неравенство (12) не имеет решений, так как 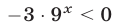 для всех
для всех 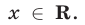 Пусть
Пусть 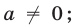 тогда, полагая
тогда, полагая 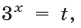 запишем неравенство (12) в виде
запишем неравенство (12) в виде
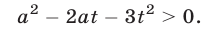
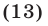
Так как квадратное уравнение 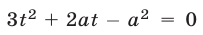 имеет корни
имеет корни 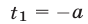 и
и 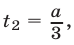 то неравенство (13) равносильно неравенству
то неравенство (13) равносильно неравенству
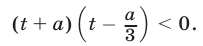
Рассмотрим два возможных случая: 
1) Если  то
то  и множество решений неравенства (14) — интервал
и множество решений неравенства (14) — интервал 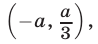 т. е.
т. е. 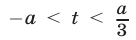 или
или 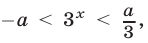 откуда
откуда 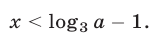
2) Если 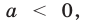 то
то 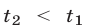 и множество решений неравенства (14) — интервал
и множество решений неравенства (14) — интервал 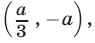 т.е.
т.е. 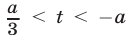 или
или 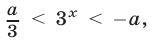 откуда
откуда 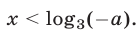
Ответ. Если 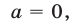 то неравенство не имеет решений. Если
то неравенство не имеет решений. Если 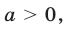 то
то 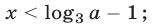 если
если 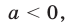 то
то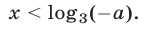
Пример №279.
Решить неравенство
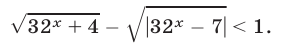
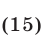
Решение:
Полагая 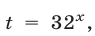 , где
, где 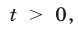 запишем неравенство (15) в виде
запишем неравенство (15) в виде
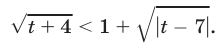
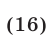
При 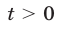 обе части неравенства (16) определены и положительны. Возводя их в квадрат, получаем неравенство
обе части неравенства (16) определены и положительны. Возводя их в квадрат, получаем неравенство

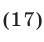
равносильное неравенству (16) при 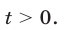
Рассмотрим два случая: 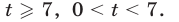
1) Если 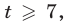 то
то 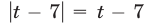 и неравенство (17) равносильно каждому из следующих неравенств:
и неравенство (17) равносильно каждому из следующих неравенств:
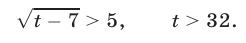
Итак, 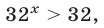 , откуда
, откуда 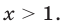
2) Если 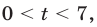 то неравенство (17) можно записать в виде
то неравенство (17) можно записать в виде
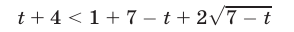
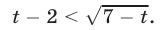
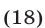
Пусть 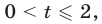 тогда неравенство (18) является верным. Пусть
тогда неравенство (18) является верным. Пусть 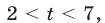 тогда неравенство (18) равносильно каждому из неравенств
тогда неравенство (18) равносильно каждому из неравенств
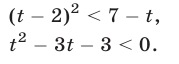
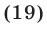
Так как уравнение 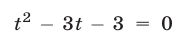 имеет корни
имеет корни 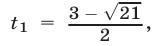
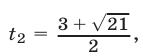 где
где 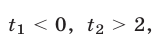 то Решениями неравенства (19) при
то Решениями неравенства (19) при 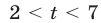 являются значения
являются значения 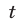 из интервала
из интервала 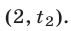 Итак, решения неравенства (18) образуют интервал
Итак, решения неравенства (18) образуют интервал 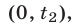 т.е.
т.е. 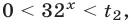 откуда
откуда 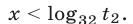
Ответ. 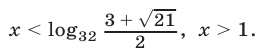
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

