Решение показательных и логарифмических уравнений основано на умении преобразовывать показательные и логарифмические выражения. Основные формулы для этих преобразований приведены на стр. 17.
Простейшее показательное уравнение имеет вид:  если
если  , то это уравнение имеет решение
, то это уравнение имеет решение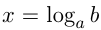 . Если
. Если  , то при любых
, то при любых  . Однако достаточно часто показательные уравнения решаются без использования логарифмов путем преобразования показательных выражений к равенству степеней с одинаковыми основаниями и затем приравнивания показателей степени.
. Однако достаточно часто показательные уравнения решаются без использования логарифмов путем преобразования показательных выражений к равенству степеней с одинаковыми основаниями и затем приравнивания показателей степени.
Простейшее логарифмическое уравнение имеет вид: 
 , где
, где  , его решение
, его решение  . При решении логарифмических уравнений очень важно помнить об ограничениях на основание и аргумент логарифма.
. При решении логарифмических уравнений очень важно помнить об ограничениях на основание и аргумент логарифма.



Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Уравнения с модулем задачи с решением |
| Иррациональные уравнения задачи с решением |
| Тригонометрические уравнения задачи с решением |
| Решение рациональных уравнений |
