Оглавление:








Пограничный слой и турбулентность
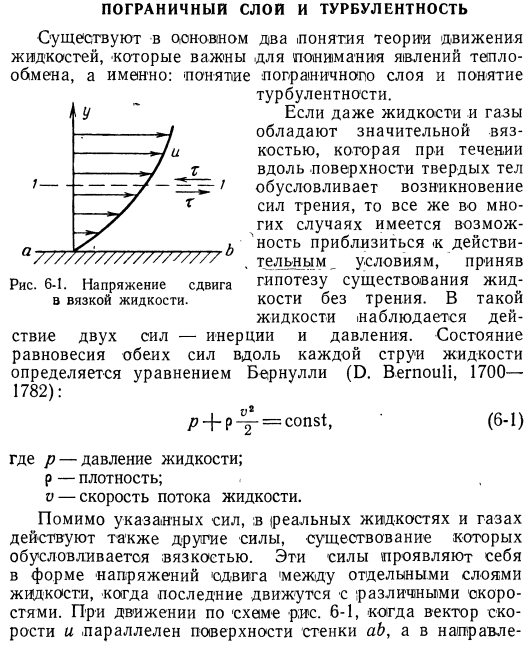
- Есть в основном 2 понятия в теории движения жидкости, которые важны для понимания явления теплопередачи. Рисунок 6-1. Напряжение сдвига в вязких жидкостях. «Концепция пограничного слоя и концепция турбулентности». Даже если вязкость жидкости или газа высока, а сила трения создается при протекании по поверхности твердого тела, во многих случаях она может приближаться. При определенных условиях принять гипотезу о существовании жидкости без friction. In такие жидкости, день и давление наблюдаются.
Жидкое состояние Действие двух сил (инерция равновесия обеих сил вдоль каждой струи) объясняется уравнением Бернулли (d. bernoulli, 1700-1782). (6-1) Где Р-давление жидкости. P-это плотность. V-расход жидкости. Кроме указанной силы, на реальную жидкость и газ действуют и другие силы, наличие которых определяется вязкостью. Эти силы проявляются в виде напряжения сдвига между отдельными слоями жидкости, когда жидкость движется с разной скоростью. Вектора скорости u-это параллельно АБ стену .
Для других типов течений уравнение напряжения трения является более сложным. Людмила Фирмаль
Для стен, перпендикулярных к ним, наблюдаются различия в скорости. Напряжение сдвига или трения m возникает в результате вязкости плоскости, параллельной стенке, например, плоскости 1-1. Значение этого напряжения задается уравнением Ньютона. Дю. (6-2) Его направление обозначено стрелкой на рисунке. 6-1. Выражение фрикционного напряжения вязкой компоненты, при нормальных условиях компоненты скорости и v, w присутствуют во всех 3 направлениях пространства, а все функции 3 координат x, y, z задаются формулой g. g. it был основан Стоксом (1845).
Согласно Стоксу, в плоскости, перпендикулярной направлению y, 2 значения напряжения трения могут быть представлены следующим образом: (6-3) (6-4) Первый индикатор при этих напряжениях m указывает, что эти напряжения действуют в плоскости, перпендикулярной y, а второй индикатор показывает направление, в котором действуют силы, вызванные напряжением act. In этот более общий случай, уравнение (6-2), а не уравнение (6-3), объясняет направление напряжения трения, показанное на рисунке. 6-1. Аналогичные напряжения трения существуют в плоскостях, перпендикулярных x и z. In в дополнение к этим напряжениям трения нормальные напряжения существуют на всех плоскостях.
Читателей, интересующихся этими отношениями, может заинтересовать граница layer. In в этой книге мы рассмотрим только поток, где простое уравнение (6-2) описывает напряжение трения с достаточной точностью. Согласно формуле (6-2), напряжение трения пропорционально градиенту скорости вдоль нормали в направлении течения. Коэффициент пропорциональности p-это физический параметр, называемый динамическим. Вязкость. Формула (6-2), кг-s1m2 или КГ! Определены размеры от s-М. В дополнение к Кинематическая вязкость, Кинематическая вязкость часто используется.
Кинематическая вязкость связана с динамическим отношением вязкости Где p-плотность. Размер кинематической вязкости составляет 1 квадратный метр в секунду. В таблице физических параметров в приложении приведены значения коэффициентов вязкости некоторых жидкостей и газов. Поскольку значения коэффициентов кинематической вязкости в некоторых справочниках задаются по абсолютной системе, т. е. Поццу (1 Пора-1 г / см * С), то часто неправильно использовать табличные данные вместе со значениями технической системы измерений.
Использование кинематической вязкости в расчетах позволяет избежать этих ошибок. Кинематическая вязкость имеет одинаковые размеры в обеих измерительных системах. По этой причине кинематическую вязкость можно найти в таблице приложений. Для жидкостей и газов, — величина коэффициента кинематической вязкости С, в основном зависит от температуры и почти не зависит от давления. Зависимость от давления начинает сильно сказываться только в районе критической точки.
Рисунок p-4 показывает этот феномен воды и пара. Все другие исследования жидкости работают примерно так же. Согласно уравнению (6-5), Кинематическая вязкость жидкости, v, практически не зависит от давления, что обусловлено незначительной степенью сжатия. Для газов, согласно уравнению состояния, оно обратно пропорционально давлению. Численное значение коэффициента динамической вязкости жидкости значительно выше, чем у gas. As для кинематической вязкости, во многих случаях наоборот true. So например, значение коэффициента кинематической вязкости воды при комнатной температуре составляет лишь 1/10 от значения этого коэффициента воздуха при той же температуре.
Поскольку коэффициент вязкости относительно мал, в потоке возникает большое напряжение трения、 Из Формулы (6-2) следует, что рост становится вялым. Такой значительный градиент скорости всегда присутствует на поверхности твердого тела в потоке. Использование трубки Пито для определения распределения скорости вблизи твердой поверхности мелассы дает кривую распределения скорости, показанную на рисунке. 6-2. На самой поверхности расход равен нулю и увеличивается с тонким слоем толщиной b до тех пор, пока не достигнет определенного значения.
Это явление, имеющее большое значение для теории механики жидкости и теплопередачи, было впервые установлено в 1904 году Людвигом Прандтлем в его знаменитой теории пограничных слоев. Терминология б. Рис. 6-2. Пограничный слой на твердой поверхности. •К основному ядру потока Прандтль также предложил тонкий слой пограничного слоя с резким увеличением скорости. Вне пограничного слоя вязкость обычно пренебрежимо мала, так как градиент скорости, перпендикулярный направлению потока, очень мал. Таким образом, поток можно разделить на 2 zones. In другими словами, уравнение.
Бернулли справедливо для каждого потока потока, потому что оно находится вне пограничного слоя, где наблюдается вязкое действие, и пограничного слоя, где поток фактически происходит без трения. То, что пограничный слой делит поток на зоны и, соответственно, изменяет режим основного ядра потока, будет рассмотрено более подробно ниже. В 1883 году Осборн Рейнольдс впервые показал, что существует 2 основных способа передвижения. Ламинарный и турбулентный flow. In в режиме ламинарного течения отдельные струи потока расположены упорядоченно параллельно друг другу, но в турбулентном режиме они хаотично переплетаются друг с другом other. In в последнем случае отдельные частицы жидкости или газа будут колебаться полностью и хаотично против определенного среднего канала.
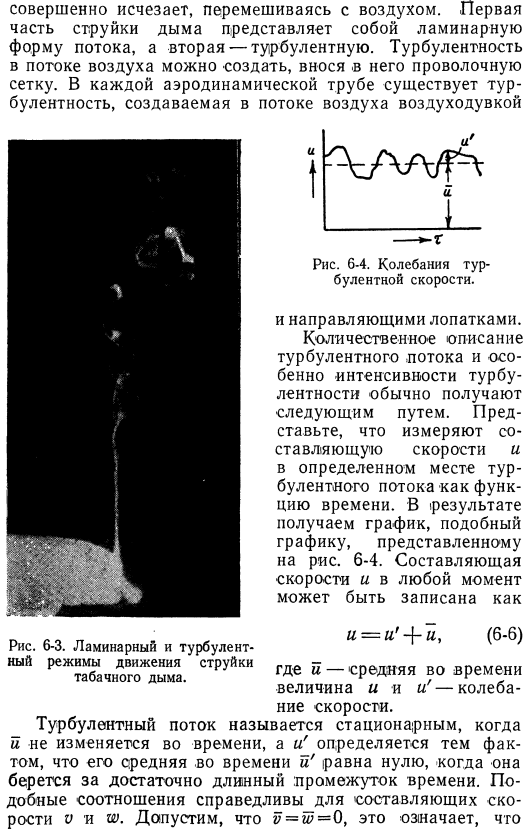
Оба режима можно наблюдать в повседневной жизни по струйке табака smoke. As вы можете увидеть 6-3, первая прямая отделка поднимется. Но она быстро становится волнистой и кудрявой, а со временем становится дымчатой Он смешивается с воздухом и полностью исчезает. Первая часть дымового потока является ламинарной, а вторая-турбулентной. Турбулентность воздушных потоков можно создать путем введения провода mesh. In каждая аэродинамическая труба, воздуходувка производит завихрение в воздушном потоке Рисунок 6-4.
- Колебания скорости турбулентности. Рисунок 6-3. Поток сигаретного дыма ламинарный поток и турбулентный режим потока. И направляющие лопасти. Количественное описание турбулентности, особенно интенсивности турбулентности, обычно получают следующим образом: Представьте себе измерение составляющей скорости в определенном положении турбулентности как функцию time. As в результате вы получите график, аналогичный показанному на рисунке 1. 6-4. Компонент скорости может быть записан в любое время следующим образом: И=и ’4-u, (6-6) Где u-среднее значение времени, а u и u-изменение скорости.
Турбулентность называется устойчивой, еслине изменяется во времени, но определяется тем, что среднее значение времени и равна равно нулю, если оно затрачено достаточно долго. Аналогичная зависимость справедлива для компонент скорости v и w. Предположим, что r7 =ω = 0. Это. .、 Средняя скорость происходит в направлении (x) .Тогда интенсивность турбулентности обычно описывается формулой: И затем Где «2-средний по времени квадрат изменения скорости u» .Другими элементами, важными для описания турбулентности, являются усредненные по времени произведения флуктуаций скорости, подобные u’v’ₜ, поскольку они связаны с турбулентными напряжениями трения .
Скорость течения на расстоянии от передней кромки пластины . Людмила Фирмаль
Это будет подробно рассмотрено в следующем разделе .В общем, рассуждения в этой книге требуют только средней скорости времени .Таким образом, символы v, w применяются до обратного хода .Конвекционная теплопередача Вайли-4 ?Турбулентность Смешанные отрицательные и движения В турбулентности flow .So .. Турбулентный теплообмен Происходит гораздо интенсивнее, чем l-xc— В ламинарном потоке. С. С. — Рисунок 6-5. С ламинарным течением Рисунок 6-5. Режим турбулентности Поверхность пограничного слоя также наблюдается в пределах полого слоя. Турбулентность в пластине. Такая боль «Теплопередача.
На поверхности плиты, параллельной потоку, происходит образование пограничного слоя, как показано на рисунке. От 6 до 5. Толщина пограничного слоя начинается от нуля на переднем конце пластины и увеличивается в направлении flow. At на некотором критическом расстоянии xc от передней кромки движение пограничного слоя изменяется от ламинарного к turbulent. As скорость потока и$увеличиваются, критическое расстояние xc уменьшается, но произведение uₛxc остается постоянным. Эксперименты, проведенные с несколькими газами или жидкостями, характеризующимися различными значениями вязкости, показали, что переход от ламинарного течения к турбулентному происходит при определенном значении безразмерного комплексного числа u₈xdv.
Это явление было впервые обнаружено reynolds. In его честь, безразмерный комплекс, полученный путем деления работы по коэффициенту кинематической вязкости получила название числа Рейнольдса или критерия Рейнольдса re. Значение числа Рейнольдса, при котором режим течения 1 изменяется от ламинарного к турбулентному, называется критическим или переходным числом Рейнольдса и обозначается rec. Более детальные исследования показали, что на критическое значение числа Рейнольдса для пограничного слоя оказывают влияние внешние условия.
Например, если ламинарный режим нарушается введением в поток решетки либо особой формы, либо шероховатости поверхности передней кромки пластины, то переход от ламинарного режима к турбулентному приведет к уменьшению числа Рейнольдса. Однако, как только эти причины турбулентности потока устранены, можно получить более высокое критическое значение числа Рейнольдса. В результате проведенных измерений Государственное бюро «эталонов» установило определенный верхний предел для пограничного ламинарного слоя потока, протекающего по плоскости plate. In в этом исследовании уровень турбулентности потока к вершине пластины изменялся систематически.
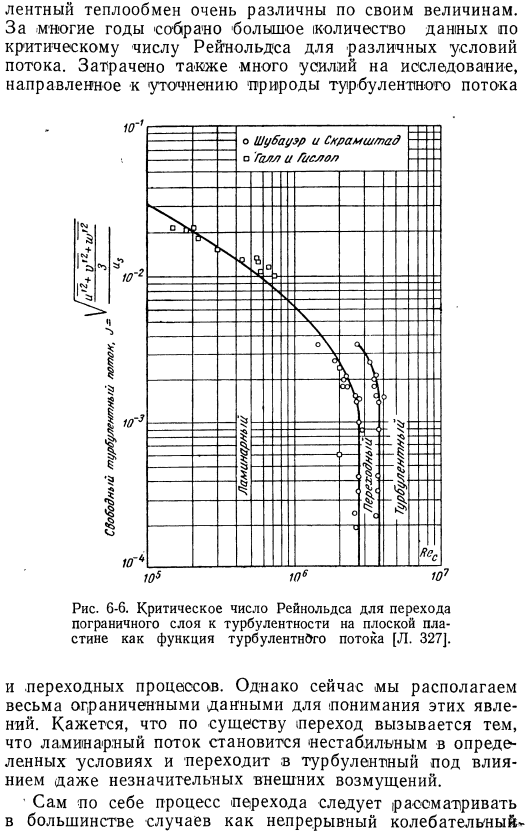
Интенсивность турбулентности-параметр, определяемый по формуле (6-7) — указывается на вертикальной оси (рис. 6-6). Критическое число Рейнольдса (rec) отображается в виде абсцисс. От 6 до 6 видно, что число переходных Рейнольдсов увеличивается с уменьшением турбулентности свободного течения. Однако это относится только к определенному уровню turbulence. At менее 0, 08% * интенсивности турбулентности, критическое число Рейнольдса не зависит от турбулентности свободного потока. Следовательно, это число Рейнольдса означает верхнюю границу ламинарного пограничного слоя на плоской поверхности. Plate. In помимо турбулентности потока, переходное число Рейнольдса зависит и от других параметров.
Например, это зависит от изменения давления и скорости потока вдоль surface. As давление уменьшается или скорость увеличивается вдоль поверхности, число Рейнольдса перехода увеличивается, но по мере уменьшения скорости вдоль поверхности критическое число Рейнольдса уменьшается. Прогнозирование условий, при которых существуют ламинарные или турбопотоки, очень важно для расчетов теплопередачи из-за ламинарных и турбопотоков. Теплопередача ленты сильно варьируется по своей величине. За эти годы было собрано большое количество данных о критических числах Рейнольдса для различных условий течения.
Немало усилий было также посвящено исследованиям, направленным на выявление природы турбулентности. Рис. 6-6. Критическое число Рейнольдса переходов пограничного слоя в турбулентность на плоской пластине как функция турбулентности[l. 327]. И переходные. Однако данные для понимания этих явлений весьма ограничены. По существу переход, по-видимому, вызван тем, что ламинарные течения становятся неустойчивыми при определенных условиях и турбулентными под влиянием незначительных внешних возмущений турбулентности. В большинстве случаев, сам процесс миграции следует рассматривать как непрерывное колебание Процесс.
Например, вы знаете, что точки перехода часто колеблются в течение длительного периода времени вблизи среднего положения. Также необходим определенный период времени. Поэтому после возникновения»первого возмущения» требуется определенное расстояние для того, чтобы кровля потока полностью установила турбулентность. Наблюдения за начальными ламинарными возмущениями привели к выводу, что»критическое число Рейнольдса»меньше, чем»измерение параметров, указывающих на установление турбулентности».
«Таким образом, различаются» нижнее и верхнее » числа Рейнольдса. 2 кривые* 6-6 на рисунке показывают оба из них values. By специальные средства, например, с использованием так называемого » турбулентного устройства (локальной шероховатости) Рис. 6-7. Движение жидкости в трубе возле входа. Отметьте положение точки перехода и ускорьте установление турбулентности. Такие методы очень полезны и часто используются в экспериментальных исследованиях турбулентного теплообмена. Состояние трубы у входа напоминает состояние продольно обтекаемой пластины. Как показано на фиг. 6-7, пограничный слой также формируется вблизи внутренней поверхности трубы, а толщина до выходного конца равна нулю, которая постепенно увеличивается по мере удаления от входного отверстия, как показано на фиг. 6-7.
Труба проходит без препятствий. На определенном расстоянии от входа lₑ, пограничный слой становится слишком толстым, чтобы заполнить весь раздел. (Направление течения перед этой точкой не изменяется (рис. 6-7), и кривая распределения скоростей не изменяется (рис. 6-7), но форма параболической или выпуклой кривой принимается в зависимости от того, находится ли движение пограничного слоя еще в области ламинарного течения или уже турбулентно). Эта часть потока называется стационарным потоком. Величин, отношение расстояния lc к диаметру d трубы, является функцией Рейнольдса number. In в области стационарного течения поток становится турбулентным, когда число Рейнольдса превышает критическое значение.
Если число Рейнольдса определяется средней скоростью u, n поперечного сечения трубы диаметром dy, то определяется критическое значение критерия Рейнольдса (формула ПЭ = — ^ = 2300. Тщательно устраняя все причины турбулентности потока, можно получить важное число Рейнольдса 500, 000, in фактических нормальных наблюдаемых условий, труба лоток становится турбулентным, когда число Рейнольдса превышает 3000.
Смотрите также:
| Движущиеся источники тепла | Уравнение количества движения пограничного слоя |
| Различные виды теплообмена | Уравнение пограничного слоя ламинарного потока |

