Оглавление:

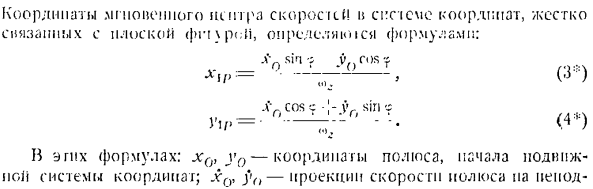








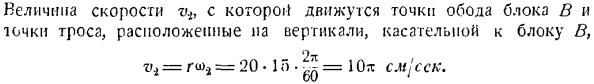













Подвижная и неподвижная центроиды
- Подвижный и неподвижный центр тяжести Геометрическое положение центра скорости планограмм, нанесенных на плоскость, называется фиксированным центроидом. Мгновенная скорость вида в плане, отмеченная на движущемся теле географическим положением центра, называется подвижным центроидом. Когда вентиляционное отверстие перемещается плоско, подвижный пентоид катится, не скользя по неподвижной пенлоиде.
Точка разделяющей сферы с подвижным, неподвижным центром тяжести теперь является мгновенным центром скорости. Центр тяжести может быть определен геометрически или аналитически. Геометрический метод нахождения движущегося и неподвижного центра тяжести заключается в следующем. In кроме того, из структуры определяется геометрическое положение мгновенного центра для заданного движения плоской фигуры, как относительно системы отсчета, так и относительно оси, закрепленной на движущейся фигуре.
Для любого положения в плане или механизме конструкция является центром мгновенного velocity Людмила Фирмаль
Аналитическое определение нейтроидов в движущемся и неподвижном состоянии осуществляется с помощью формул, дающих координаты мгновенного центра скорости. Координаты центра мгновенной скорости в системе фиксации оси представлены следующим образом: хр = х0-г ^,(я *) Дж ’/’ — П ’ О «(2 *) L A в направлении скорости ce, т. е. радиуса OA или его продолжения. Стержень AB будет скользить под углом D, но не будет отрываться от стержня, а скорость точки стержня все равно будет соответствовать точке Z, но будет ориентирована вдоль стержня.
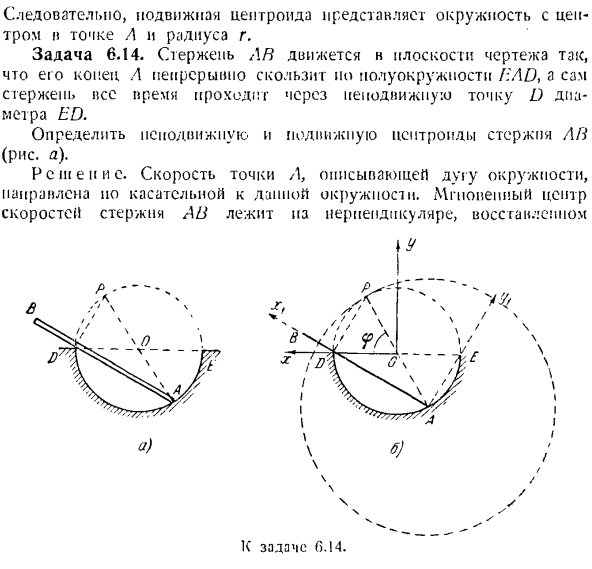
Если восстановить перпендикуляр стержня в точке D, то найдем точку пересечения перпендикуляров со скоростями точек A и L, то есть мгновенную скорость центра стержня AB в точке P. Так как прямой угол ADP основан на диаметре AP окружности, то эта точка находится на окружности HAD. Таким образом, мгновенный центр P скорости при движении стержня AB перемешивается по периметру PDAH.
- Таким образом, момент, отмеченный в фиксированном пространстве геометрическим расположением центра, является окружностью центра O и радиусом OA. Это центр тяжести фиксирующего стержня. Движущийся центр масс-это геометрический локус мгновенного центра масс, отмеченный в плане движения. Точка P расположена на некотором расстоянии AP = 2-OA от точки стержня A. Итак, точка P представляет собой окружность вокруг движущейся точки A, окружность с радиусом, в 2 раза превышающим полукруглый радиус EAL.
Найдите уравнение центра тяжести. C. Для этого выберите 2 системы координат: неподвижные оси с точкой O в качестве начала координат, ось l * вдоль диаметра лекарственного средства, указывающая влево, ось y направлена вертикально вверх, точка A в качестве начала координат перемещается, ось x {стержень AB, ось-прямая к стержню AE (вертикаль). в этом случае уравнение неподвижного центра масс будет иметь вид: 4 — > > 1 =Γ\ Уравнение перемещения центра тяжести Р. В? р = 4 РС.
Это центр тяжести подвижного стержня. Людмила Фирмаль
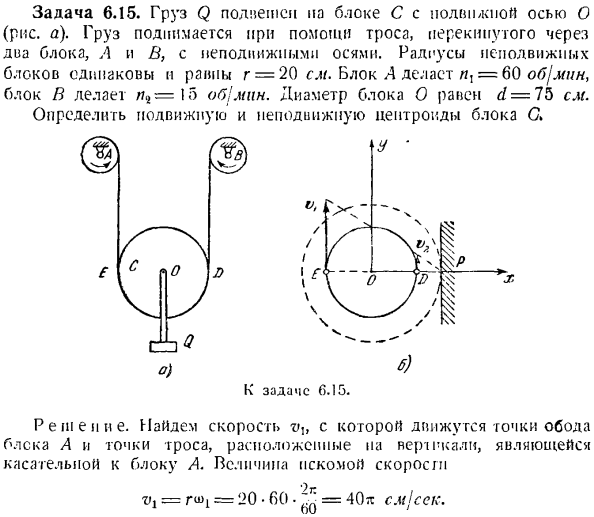
Задание 6.15.Нагрузка Q смешивается с подвижной осью O в блоке C. (рисунок A).Груз поднимается с помощью недостижимой оси путем привязки блоков A и B. радиус неподвижного блока одинаков: r = 20 см. Блок A-это I = 60 об / мин, блок B-ni = \ o об / мин! Диаметр блока O равен d = 75 см. Определите подвижный и несфокусированный центроид блока С. Задание 6.15 к. Re e и e. найти точку обода блока A и скорость, с которой движется точка троса на вертикальной линии, соприкасающейся с блоком A. x>,= = 20 * 60 * = 40l см / сек Скорость, с которой точка троса перемещается, vif, по точке обода блока B и вертикальной касательной блока B П2 = = 20•1 О•^ Р = Ил cMj’cick.
Эти скорости являются скоростями точек E, D блоков C, где кабель спускается по касательной от обола (рисунок B).Поэтому известь:.!2-точечная скорость, E и D в плане этажа. Эти скорости параллельны друг другу и перпендикулярны линии ED, соединяющей обе точки. Мгновенный центр скорости блока находится на пересечении вертикальных линий и восстанавливается до скоростей E и D.
In в данном случае эти вертикальные линии совпадают. Тем не менее известно, что скорости точек E и D достаточно велики, чтобы определить положение мгновенного Центра. Эти скорости пропорциональны расстоянию от точек Е и о до мгновенного центра velocity. So, если обозначить неизвестное расстояние от точки D до мгновенного центра скорости P через/(рисунок B), то получим: вл-(д /О), У = / у>. если мы решим 2 уравнения Эйна вместе、 / = — Dvj_ _ _ 25 SM(1)
Для этого нужно установить оба конца и V. lt на выбранную шкалу и соединить оба конца по прямой line.速度v. lt из подобия треугольников, образованных tfj и этими линиями、 DP I _ v * ’»- г. — •.Или -; -, -. -’、 л. с. уть е \ −1 Вт’ (1) чтобы соответствовать. Как только положение центра скорости в данный момент определяется произвольно! Узнайте о положении блоков, неподвижных и подвижных цепных средств. Выберите фиксированные оси.
скорректируйте ось x горизонтально вправо и направьте ось y вверх вдоль прямой линии, по которой движется ось движущегося блока. При подъеме груза мгновенный центр скорости Р перемешивается в прямом неподвижном пространстве параллельно оси продольной оси. Эта линия является Ронды еще нет. Мысленно увеличьте размер блока, начертив круг радиуса, чтобы найти центр тяжести в движении.- [■- Y центрируется O.
As в результате окружность с радиусом 1-y, y с центром O является подвижной nenrj o- Идея-момент, обозначенный на плане этажа для перемещения геометрического расположения центра. Движение Блока О можно представить как вращение без скольжения вертикали, проходящей через точку Р, вдоль подвижного центра тяжести, радиуса окружности-покоящегося центра тяжести. Задача 6. 16.Концевая часть стержня8d подвижно прикреплена вместе с ползунком B горизонтальной направляющей.
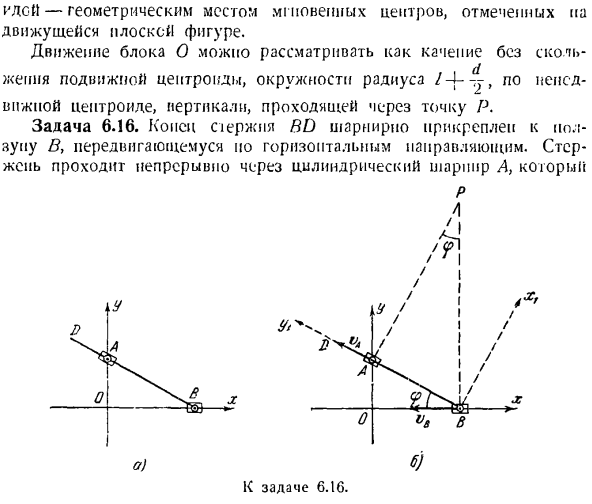
Стержень непрерывно проходит через цилиндрическое соединение А. П. С. 4. Задача 6.16. Вы можете вращаться вокруг оси, перпендикулярной плоскости изображения. Расстояние Оа-а(рисунок а). Найдите уравнение для неподвижного центрального стержня и подвижного центрального стержня. Обратите внимание, что механизм, рассматриваемый в вопросе роли, называется когоидным графом. Он рисует геометрическое расположение прямого липового конуса, то есть радиус-вектор прямой, увеличенный или уменьшенный на тот же отрезок.
Решение. Выберите фиксированную систему координат с центрами и точками O. направьте ось x горизонтально вправо. Это соответствует направлению движения слайдера B. it имеет ось y, но движется вертикально вверх(рис. 6). При любом положении стержня VG), определяемом углом (рис. б), путем построения точки Р-находим мгновенный центр velocity. To сделайте это, восстановив перпендикуляр к направлению скорости точки B. точка B движется линейно вдоль оси x, поэтому ее скорость направлена вдоль этой оси
. Вертикальная ось BP параллельна оси Y.2-я точка стержня, где направление скорости известно, является точкой, которая в настоящее время проходит через цилиндрический шарнир A. скорость точки, проходящей через стержень Неподвижная точка а (рисунок б) направлена вдоль стержня. Восстановите перпендикуляр. Точка р на пересечении этих перпендикуляров является мгновенным центром скорости. Найдите координаты точки P, чтобы определить фиксированные центроиды, то есть мгновенное метрическое положение Петра, отмеченное фиксированной гранью.
И Но… Я, ээ… (2) Сири о Син-о сирр ’ о Потому что угол AP B = o. за исключением угла-f, разрешает эти очки вместе. Из первого уравнения Из 2-го уравнения Сэр? Шин! х)> = а {Ур-а). О Следовательно、 Координаты мгновенного быстрого титра в СМ этих координат строго связаны с плоским предложением и выражаются следующей формулой: йф ^грех? В Потому что Сильф 0… (3 секунды) д \ _ соя с!-1 ′ грех » В этих формулах x0, y0-координаты полюсов, начало подвижной системы координат. x (), y () — проекция полярной скорости на i-й узел. Это экю.
Исправлено уравнение центра тяжести. Неподвижные центроиды-параболы с осями, параллельными оси Y. Перейдем к определению уравнения движения центра масс. Начальная точка и точка выберите неподвижную неподвижную систему координат со стержнем / 3D в футах. Ось _yt ориентирована, но для стержня W) ось xy перпендикулярна стержню(рисунок B). Найти координаты центра мгновенной скорости в движущейся системе координат. х, = ВР * да? = с COS <?,(3) Ил = АВ =-. (4) 1 знак Из Формулы(4) находим sin <p =-и вводим угловое значение ego в уравнение (3).Что купить: = nyj = i 1 / — JZ?、 1 А-Р А ф г-ХГ Где вы находите уравнение подвижной центроиды * ) 4 O / O <1 \ \ СХ = Йи(г \ л «). Для решения этой задачи мгновенные координаты центра скорости неподвижной и подвижной осевых систем были выражены параметрами.
Время. Из условий задачи невозможно найти временную зависимость угла_ G silsil 2 Из треугольника ABC, используя ту же теорему、 Потому что вы пострадали от углового CAD.Если сравнить равенство (I) и равенство (2), то получится следующее: , как VJ * ^Ь г’- Или У = — (3) С другой стороны, если мы используем теорему Косинуса из треугольника LR / J、 г * = р+ АР-2yag с COS <Р. (-1) Квадрат (3) и поместите это значение в Формулу(4).Затем получать: Б] (р-а) «= р» 2 а *-2ar COS в -2brt потому что б.((>) Умножает выражение (o) на 2 и подставляет значение (y + b)в выражение (6).У нас есть: потому что.
Или, после простого преобразования、 лаборатория _ ’ПБ-стоимость、) Эго представляет собой уравнение движущегося центра тяжести в полярной системе координат, центр которой совпадает с точкой движения B, а угол поворота радиус-вектора измеряется от движущейся линии BC. Задача 6.18.In в шарнирном квадрате предыдущей задачи, где обе стороны равны паре, угловая скорость кривошипа AB равна o) 0.
Угловая скорость кривошипа постоянного тока и скорость точки С в момент, когда все 4 стержня вытягиваются на 1 прямую. The solution. In в предыдущей задаче было получено уравнение подвижного центра тяжести стержня летательного аппарата 2а, ч T / = 5LG — и cos b)> Где= VO-расстояние og от точки B до мгновенного центра скорости. Если стержень Rce вытянут на 1 прямую, то угол принимает значение r, расстояние до мгновенного центра скорости в этой точке или значение точки B 2 АВ Мгновенный центр скоростей на расстоянии е или точка c «1 тонна. б я-Л Г ’ — Г> «Я-б = хли-а-
Скорость точки B, которая принадлежит кривошипу AB, равна ВН = АО> 0. Эго-это скорость точки Б, так как она принадлежит солнечному стержню, райне Если мы сравним эти значения скорости точки B, то получим мгновенную угловую скорость стержня BC. … _ <Б-а) мг ~ ~ г, 27; Здесь коэффициент скорости точки С получается как произведение мгновенной угловой скорости и мгновенного радиуса стержня БК. Величина угловой скорости кривошипа постоянного тока равна отношению скорости точки С к длине кривошипа в — (°о(б-я) CD-направление угловой скорости’ 2b ’ (I) CD соответствует a> 0.
Для приобретения я решил не просить ни определения центра тяжести плана этажа.«Сборник задач теоретической механики» И. В. Мещерского, а также зд А. И. 1950 и позднее: о43, 546,548, 550, 552,553. Важная ось; ), (2) вместе и исключите время, вы найдете уравнение фиксированного центра тяжести.Решите систему уравнений(3 ), (4) и исключите время, чтобы определить связь между координатами x1p и y1p, то есть уравнение движущегося центроида вещественной формы
Для некоторых задач удобнее использовать полярную систему координат для нахождения фиксированного центроида и движущихся центроидных уравнений. h. при решении задачи i, после таких действий, рекомендуется определение подвижного и неподвижного центра тяжести. 1) Выберите план этажа, необходимый для нахождения фиксированного центроида в движении. 2) Выберите 2 системы координат, которые являются неподвижными и подвижными, прочно связанными с плоскостью
перемещения (рис. 3) построить или использовать формулу (I), (2), чтобы найти мгновенный центр скорости любого положения в плане этажа. 4) мгновенная скорость в фиксированной системе осей делает координаты центра зависимыми от любых переменных параметров движения. о) совместно определяются координаты мгновенного центра тяжести С целью исключения явных уравнений переменных и стационарных центроидов. в) формула(.4), (4) или геометрической конфигурации, используя мгновенный центр скорости m,
сравните мгновенные координаты спидометра движущейся системы координат с некоторыми переменными параметрами движения. 7) решите эти уравнения вместе и исключите переменные параметры, чтобы определить уравнение подвижного окружного фонда в явном виде. Задача 6.13.Механизм коленчатого вала (рисунок O) состоит из кривошипа OA_r, шатуна AB_1 и ползуна I», вращающегося вокруг неподвижной точки O и перемещающегося по прямой Ox.
Угол поворота кривошипа равен/<*/.Где k-постоянный коэффициент. Найти все неподвижные и подвижные уравнения сетрода шатуна в параметрической форме. Решение.Фиксированная система координат xy с начальной точкой O и системой координат xxu\, в точке A принадлежащей Шатуну, патч.используйте m для выбора.ось xY направлена вдоль шатуна AB (рисунок B). Найти координаты точки А. ХД-г соз Ф = G соѕ kty йа = Р грехе 0 = г грех / гл Вычислите производную от координат точки А и определите проекцию скорости на неподвижные оси. ХЛ =-ГК греха КТ, йа-гр, потому что в ХТ. Чтобы найти мгновенную угловую скорость шатуна, представим ординату точки A от угла поворота шатуна cp(угол
* 1 = Ajj = — 7- нет. Если ввести это значение в Формулу(1), то: Теперь, используя равенство (1), (2), мы находим уравнение pep ) и (4) это выглядит так: р и. г. ФК 、 | вл—Ри-ВКИ-Р / Я Грех Грех КТ КТ г -] — РК, потому что КТ ——„- * * «- ^- 7ПШ — — -1111-Ри я. * Я> В1 ′ — Р1 sill2 КТ. мы фабрика начала Китая. и… подоконник РК / ТФ -:, * что / ТФ•—грех КТ _ Г= —— / —— я -} /> — Г4SinU /、 » потому что ИД РК Или после простого упрощения、 А, Г. IrJ, КТ \ * ИС = \ сихъ р-б -/’* Jfsp = тг»(/- J-в пысиным лит г л * — г * sin4 КТ. Эти уравнения являются уравнениями движущегося центроида в параметрической форме. для R=/.Уравнение движущегося центра масс хы, з = р(я −2 греха * — т)= р потому что 2kty г \ п = 2р грех КТ, потому что КТ = Р грех 2kt, или без учета времени
В результате центр масс в движении представляет собой окружность с центром в точке А и радиусом R. Задача 6.14. Так как стержень АВ движется по плоскости чертежа, то его конец непрерывно скользит по полукругу BAD, а сам стержень всегда проходит через неподвижную точку D с диаметром ED. Определите неподвижный и подвижный центр тяжести стержня АВ (рисунок а). Расширение: скорость точки A, которая представляет собой дугу окружности, направлена к указанной окружности, но является касательной. Мгновенный центр скорости стержня AB находится на восстановленном перпендикуляре. Задача с. 14. один.)
Смотрите также:
Предмет теоретическая механика
| Уравнения плоского движения твердого тела. Уравнения движения точки плоской фигуры | Ускорение точек плоской фигуры |
| Скорости точек плоской фигуры | План скоростей и план ускорения |

