Оглавление:









Подобие процессов массообмена и теплообмена
- Если массовое содержание компонента 1 мало по сравнению с 1, то в формулах (16-27) и (16-28) термин vw равен negligible. In в свою очередь, обе эти формулы принимают тот же вид, что и соответствующая формула теплопередачи (7-2). Для наглядности сравним эти уравнения. Уравнение теплового потока : Уравнение массового расхода : Сходство этих уравнений и их решений должно быть одинаковым. Поэтому решение дифференциального уравнения течения может служить решением уравнения массопереноса.
Все, что нужно для этого, — это заменить коэффициент диффузии a вместо массового содержания, коэффициент термодиффузии d вместо температуры t. Существует также Сходство между общим уравнением теплопроводности (без диссипационного члена) и уравнением массопереноса с определенными свойствами. В разделе 9-1 температурное поле вблизи геометрически подобного объекта имеет вид.
Если параметр имеет одно и то же значение, не зависящее от размера любой выделенной части равновесной системы, то он называется неаддитивным или интенсивным, если же значение параметра пропорционально размеру части системы, то он называется аддитивным или экстенсивным. Людмила Фирмаль
Эксперимент 1hazer[l. 285], проведенный при конденсации пара в смеси пара и воздуха, полностью подтверждает приведенные выше пропорции. Процесс принудительной конвекции на малых скоростях может быть описан следующей формулой: /. Ре= з’, Ре, пр), (16-33) Где o ’ — безразмерная величина, деленная на разность между температурой t точки На безразмерном расстоянии y от поверхности тела и температурой точки, определяющей условие, деленной на разность температур, определяющую условие, например t₈ и tw; re разности между самой температурой и расстоянием от тела — тест.
Рейнольдса, и y / если разность температур для одного и того же объекта заменяется разностью парциального давления или массового содержания: «’Я = (а-’>-wₗw) л (wᵢₛ-wₗₐ) ; Р = (pᵢ-pₗw) л (pₗₛ-pₗw) и температуропроводности а-коэффициент диффузии Д, парциальное давление или массовый контент, написанный, чтобы получить формулу. Ж ’= 1 (х’, г’, р’, ре -^ -) == / (х’, г’, з’, Ре Ка) (16-34) Безразмерная величина v / d называется критерием Шмидта. Функция f имеет одинаковую форму как в выражении (16-33), так и в выражении (16-34). Количество значений Шмидта показано в таблице. P-9. In в случае Газа число Шмидта не зависит от давления.
С температурой, иногда она также изменяется в зависимости от концентрации. В области теплопередачи нас в первую очередь интересует тепловой поток qw на единицу площади поверхности тела. Следующая формула может быть рассчитана с использованием коэффициента теплопередачи А. С другой стороны, есть такое выражение Отсюда Аналогичным образом можно определить коэффициент массопереноса hd, используя характеристики потенциала процесса массопереноса.
К сожалению, нет общей точки зрения на то, какие параметры следует использовать для выражения возможности передачи. Используйте массовое содержание для определения коэффициентов массопереноса из уравнения mᵢw= 9hd (w {w-wₗₛ). (16-36) ) Для жидкостей с почти постоянными характеристиками (p ^ const) массовое содержание можно заменить определенной плотностью, и уравнение примет вид: (? Ив ПЛС) ’ Или, в грамме молекулярной плотности, разделив последнее уравнение на молекулярную массу, это выглядит так: В дополнение к предположению const, предположим, что разность температур в поле мала по сравнению с абсолютной temperature. As в результате получаем следующую формулу: фл. Это уравнение было впервые названо e.
Оно было выведено Далтоном (1788). Последние 3 уравнения чаще всего встречаются в литературе. При указанных выше условиях коэффициент массопереноса одинаков для всех уравнений. Однако коэффициенты массопереноса для этих уравнений различны, когда существуют большие вариации температуры, давления и характеристик. Для низкой конвективной скорости v массовый поток на поверхности твердого тела или на границе раздела может быть выражен формулой (16-7).
Если мы добавим это выражение к уравнению (16-36), то: (iso (16-36а) Взяв безразмерный перепад температуры 0 ’и безразмерное расстояние y’ = y / 1 от твердой поверхности, можно преобразовать уравнение (16-35) и получить безразмерное уравнение коэффициента теплоотдачи. А / _ / (нет. «х ’» Или, согласно формуле особого положения вдоль поверхности тела (16-33), последняя формула принимает вид: 4 = / (Ре, РР). (16-37).
Аналогично, разделив массовое содержание, можно получить формулу коэффициента массопереноса безразмерной [опорная Формула (16-36а) ] разности-w | for, а также координаты y на определяющем отрезке/. (16-38) если дифференцировать дифференциальное уравнение (16-34) относительно y и принять* / = 0, то получим: = = Южная Каролина.) (16-39) Функции f уравнения (16-37) и (16-39) аналогичны. Таким образом, уравнение части b, связанное с теплопередачей ламинарного потока, заменяет эталонное nus> selta al / ’ k безразмерным коэффициентом массопереноса adz / z, и если эталонное v / a Прандтля безразмерно, дает адекватное решение задачи переноса вещества? Значение v / d.
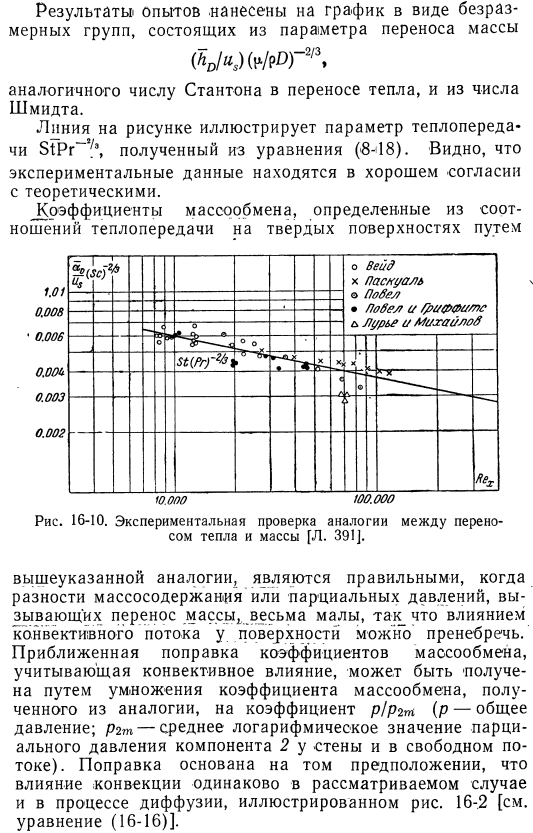
Этот закон есть. Поток л. Трубка и. Ряд экспериментов по массе потока также подтвердил турбулентность. On_ плоская пластина, и _for flow. .It проходит через цилиндр, вокруг сферы, и через закрытый layer .As в качестве примера на рис .16-10 приведены результаты экспериментов по испарению различных жидкостей с плоской поверхности в воздушном потоке[L .286] .Результаты эксперимента построены в виде безразмерной группы, состоящей из параметров массопереноса (V » ₛ) (^r2/3) .От числа Шмидта аналогично числу Стантонов в теплопередаче .Линией на рисунке показан параметр теплопередачи STPR — ^3, полученный по формуле (8-18) .
- Экспериментальные данные хорошо согласуются с теоретическими данными. Коэффициент массопереноса, определяемый по коэффициенту теплопередачи на твердой поверхности Рис .16-10 .Экспериментальная проверка сходства теплопередачи и массопереноса[л . 391] .Приведенная выше аналогия верна, если разница в массовом содержании или парциальном давлении, вызывающем массоперенос, очень мала, поэтому эффект конвекции на поверхности пренебрежимо мал .
Приближенная коррекция коэффициента массопереноса с учетом эффекта конвекции получается путем умножения коэффициента массопереноса, полученного по аналогии с коэффициентом p / pg (p-общее давление, pg ?N-средний логарифм парциального давления компонента 2 вблизи стенки и в свободном пространстве потока) .Эта поправка основана на предположении, что эффекты конвекции одинаковы в рассматриваемом случае и в диффузионном процессе, показанном на Рис .5 .16-2 [справочная формула (16-16) ] .В . Рис .16-11 .
Описанное таким образом состояние называется макроскопическим состоянием, и законы термодинамики позволяют установить связь между макроскопическими параметрами. Людмила Фирмаль
Упрощенная схема турбулентного массообмена .Эксперимент с mikulía{L .287] и Hazer показывают, что эта поправка удовлетворительна для ламинарных и турбулентных течений вдоль плоской пластины, когда число Шмидта очень близко к 1 .Для газовой смеси, если коэффициент диффузии D равен коэффициенту температуропроводности a, оба вышеуказанных безразмерных коэффициента равны для конкретного значения критерия Рейнольдса .Коэффициент диффузии D вместо коэффициента диффузии a = X / P cp= !При замене Cp (Cp-удельная теплоемкость единичного объема при постоянном давлении) происходит следующее .
Эта формула выведена Льюисом и называется Мнение Льюиса [L . A .288] .в турбулентном обмене существуют следующие условия (рис .16-11) : V ’объем газа, перемещаемого между плоскостями 1 и 2 за единицу времени через единицу площади, и t ’и I’ и W ’ — выраженные в терминах температуры и массового содержания рассматриваемой плоскости .Тепловой поток от плоскости 1 к плоскости 2 за счет турбулентного обмена выражается следующим образом: = (16-41) Если этот тепловой поток выражается с помощью коэффициента теплопередачи a, то: ^ t-t.) = ^ V, Cₚ (t-V) .(16-42).
Массовый расход на единицу площади при том же турбулентном обмене имеет следующие значения:* ш’, (16-43) Коэффициент турбулентного массопереноса (hDₜ>) лапа (ж, — СШ) = ПВ ’ (ж, — а «’.) .(16-44) Термин для деления уравнения на уравнение (16-42) (16-44) имеет вид: = (1§ −45) Это указывает на то, что отношение Льюиса справедливо для турбулентности, независимо от того, равно ли отношение A / D 1 .In в случае ламинарной субструктуры, всегда присутствующей в турбулентном потоке вблизи поверхности твердого тела, соотношение Льюиса является !Действует только для D — .
В разделе 8-4 турбулентные тепловые потоки были выражены следующим образом: dt .4Т-экв ?Срди .Турбулентная тепловая диффузия заменяет коэффициент температуропроводности в уравнении ламинарного теплового потока .Аналогичное уравнение для турбулентного массопереноса можно получить, заменив коэффициент диффузии D в уравнении (16-7) на коэффициент турбулентной диффузии eD в массе .Очевидно, что в случае ep8d, формула (16-45) держит .Из теоретических соображений следует ожидать, что это case .As в результате эксперимента IB был получен в соотношении чуть большем, чем 1 .
Как уже упоминалось в § 9-1, теплообмен при условии естественной конвекции определяется по формуле: Ню = ф (г, пр), (16-46) Где Nu-безразмерный коэффициент теплопередачи-u .Критерий гр-глашова[gP (fw -^) / *] / * ’; Pr — прандулярный критерий v / A .В Формуле критерия глашова произведение объемного коэффициента расширения р и определяющей разности температур tw-t определяет отношение плотности (п — ПМ) /pₑ- Для массообменных процессов, в которых подъемная сила обусловлена различиями в плотности различных смесей, удобно записать критерий глашова в виде: Где плотность газовой смеси вблизи стенки ?
Плотность газовой смеси вне пограничного слоя .Аргументы, аналогичные тем, которые применяются к условиям вынужденной конвекции, приводят к следующей формуле для коэффициента массопереноса: = Ф (0rD> -£ -) = / (ОГА, СК) .(16-47) В этом случае функция / аналогична соответствующей функции в области теплопередачи .Если процессы теплопередачи и массопереноса протекают одновременно, то коэффициент массопереноса можно определить при условии D =£a путем решения соответствующей задачи из области теплопередачи .Пример 16-2 .
На поверхности воды поток воздуха движется со скоростью u * = 3, 1 м / с .необходимо определить количество воды, которое испаряется с поверхности от 1Л12 до 1 часа .Температура поверхностных вод составляет 15°с .Температура воздуха 20°С; парциальное давление водяного пара в воздухе Р » = 0, 00792 к’г /см2, что соответствует содержанию влаги f = 33, 3% .Длина водной поверхности в направлении движения воздуха составляет х-100 лм = 0, 1 м .Стандарты Рейнольдса воздушного потока В 3 .1-0 .1 платформе rcx-в—1 .56-10- ⁵ (v = 1, 56-10″ ’ м2 / с берется из таблицы приложения) .
Так, коэффициент флюс-ламинарного и среднего теплообмена определяется по формулам (7-14) и (7-15) .Nuₓ= 0 .664] ^ PrKReₓ .Коэффициент массопереноса определяется из аналогичного уравнения ч ^ х / Д = 0 .664 ^ * 7/5 Коэффициент диффузии D = 0, 09504 м2 / ч (см .Приложение) .Отсюда В _15 .61 О-’ .36OOP₁ 0 .09504 * ⁰11、 Д .Так .. = o, g64 / zo, 591 v19830 = 78, 4. И затем 78, 4-0, 09504 ₜ БГ—6-я — — — — — — — -⁼⁼, ⁵m > цек ’ При использовании коэффициента Льюиса необходимо сначала определить коэффициент теплопередачи.
Случай воздуха пр = 0. 710、 nuₓ= 0. 624 ^ t9 ′ 830 / z07to = 83. 3; ___ _83. 3-0. 022 а = nu_ *. (А / Л — ’ = — Д- — — — = 18. 35 ккал! М2-ч * счастливый. 20°c и 1 кг! Для воздуха в см2 удельная теплоемкость установки составляет 18, 35 Объем составляет 0, 28 ккал / м3 * град. Следовательно, hₙ — — q-gg — = 65, 5 м / ч. Это значение на 13, 8% меньше предыдущего из-за того, что предположение о том, что отношение a / d равно единице и отношение Льюиса справедливо, в данном случае неверно.
Однако для приблизительного расчета испарения влаги в воздух вполне подходит коэффициент Льюиса. Парциальное давление водяного пара на поверхности воды равно давлению насыщения при температуре над поверхностью воды. П ш = 0. 01735 до g1cm2. Отсюда находим количество воды, которое испаряется с поверхности 1м2 за 1 час[справочная формула (16-36)]: качестве hd, 74. 5 ювп> — −47.
Смотрите также:
| Ламинарный пограничный слой на плоской плите при переносе массы и тепла | Испарение воды в воздух |
| Интегральные уравнения диффузионного пограничного слоя | Теплообменники |

