Задача №51.
По внешней стороне параболы с горизонтальной осью, уравнение которой 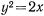 , скатывается без трения и без начальной скорости шарик, начальная ордината которого
, скатывается без трения и без начальной скорости шарик, начальная ордината которого 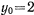 . В какой точке шарик соскочит с параболы?
. В какой точке шарик соскочит с параболы?
Решение:
Пусть положительная ось 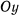 направлена вертикально вверх. Движение шарика будет определяться интегралом живых сил, который имеет вид
направлена вертикально вверх. Движение шарика будет определяться интегралом живых сил, который имеет вид
постоянная живых сил 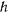 при заданных начальных условиях будет равна
при заданных начальных условиях будет равна  . Тогда скорость определится уравнением
. Тогда скорость определится уравнением
Для определения момента отрыва шарика от параболы воспользуемся естественными уравнениями движения. В проекции на нормаль будем иметь
В момент отрыва 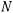 обращается в нуль. Для определения радиуса кривизны
обращается в нуль. Для определения радиуса кривизны
воспользуемся уравнением кривой. Будем иметь
где 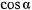 — косинус угла наклона касательной к параболе
— косинус угла наклона касательной к параболе
Подставляя эти значения, будем иметь
После подстановки значения 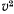 и сокращений приходим к уравнению
и сокращений приходим к уравнению
Нетрудно видеть, что единственным действительным корнем этого уравнения является значение  . Это и будет то значение
. Это и будет то значение 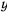 , при котором точка отрывается от параболы.
, при котором точка отрывается от параболы.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №49. Материальная точка массы описывает окружность радиуса , притягиваясь некоторой точкой этой окружности. Найти силу притяжения и скорость точки в зависимости от расстояния точки от . |
| Задача №50. Тяжелое колечко массы надето на гладкую вертикально расположенную проволочную окружность радиуса . Колечко может свободно передвигаться по ней. В начальный момент оно находится в самой нижней точке окружности и ему сообщена начальная скорость . Найти условия, при которых колечко совершит полный оборот по окружности и определить давление на нее колечка, когда оно находится в самой верхней ее точке. |
| Задача №52. Тяжелый шарик, масса которого равна , нанизан на горизонтальную проволочную окружность радиуса с коэффициентом трения . Определить, какую начальную скорость нужно сообщить шарику, чтобы он сделал по окружности один полный оборот. |
| Задача №53. Тяжелая материальная точка движется по внутренней поверхности прямого кругового конуса, вершина которого обращена вниз, а ось симметрии вертикальна. Угол при вершине равен . В начальный момент расстояние точки от вершины конуса равно , начальная скорость равна и направлена перпендикулярно к образующей конуса. Определить траекторию точки и давление, которое она оказывает на поверхность конуса. |

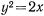 , скатывается без трения и без начальной скорости шарик, начальная ордината которого
, скатывается без трения и без начальной скорости шарик, начальная ордината которого 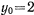 . В какой точке шарик соскочит с параболы?
. В какой точке шарик соскочит с параболы?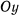 направлена вертикально вверх. Движение шарика будет определяться интегралом живых сил, который имеет вид
направлена вертикально вверх. Движение шарика будет определяться интегралом живых сил, который имеет вид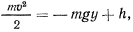
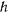 при заданных начальных условиях будет равна
при заданных начальных условиях будет равна  . Тогда скорость определится уравнением
. Тогда скорость определится уравнением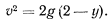
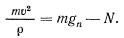
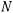 обращается в нуль. Для определения радиуса кривизны
обращается в нуль. Для определения радиуса кривизны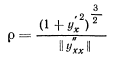

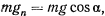
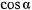 — косинус угла наклона касательной к параболе
— косинус угла наклона касательной к параболе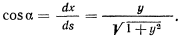
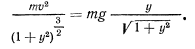
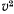 и сокращений приходим к уравнению
и сокращений приходим к уравнению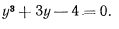
 . Это и будет то значение
. Это и будет то значение 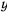 , при котором точка отрывается от параболы.
, при котором точка отрывается от параболы.
