Задача №18.
По неподвижному круговому конусу с углом при вершине, равным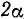 
, катится без скольжения другой круговой конус с углом при вершине, равным 
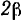, так, что ось симметрии последнего вращается вокруг оси симметрии не-подвижного конуса с постоянной угловой скоростью ooj. Определить абсолютную угловую скорость вращения подвижного конуса и найти аксоиды.
Решение:
Подвижный конус катится по неподвижному без проскальзывания так, что точки подвижного конуса, расположенные па общей образующей, имеют нулевые скорости. Поэтому мгновенная ось вращения совпадает с общей образующей обоих конусов. Во время движения мгновенная ось вращения перемещается как по поверхности неподвижного, так и по поверхности подвижного конуса. Поэтому аксоидами будут являться эти же самые поверхности конусов. Движение подвижного конуса теперь можно’представить как сложное, состоящее из вращения подвижной системы вокруг оси симметрии неподвижного конуса с переносной угловой скоростью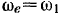 
(рис. 59) и относительного вращения подвижного конуса вокруг своей оси симметрии в подвижной системе координат. Зная направления абсолютной и относительной угловых скоростей подвижного конуса, а также величину и направление переносной угловой скорости, легко определить величину и направление абсолютной угловой скорости вращения конуса. Из треугольника скоростей будем иметь
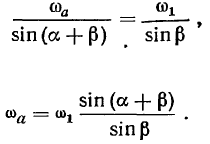
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
