Пример решения задачи №20.
Пловцу предстоит переплыть реку шириной Н из точки М в точку N (рис. 4-9). Расстояние от точки О, расположенной напротив точки М; до точки N равно Z, скорость течения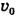 
. С какой минимальной скоростью относительно воды 
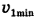пловец может плыть, чтобы попасть в точку N на противоположном берегу?
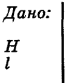
Решение:
Давайте подумаем, что означают слова «минимальная скорость пловца относительно воды». При каком соотношении между
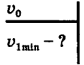
скоростью течения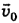 
скоростью пловца относительно воды 
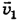и скоростью пловца относительно берега 
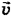вектор скорости 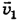будет минимальным?
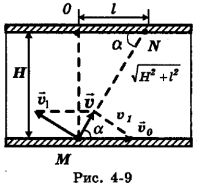
Обратимся к рис. 4-9. Скорость реки 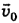нам дана и даны стороны треугольника MON, значит, задан угол 
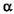, определяющий направление вектора скорости 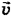относительно берега, т. е. угол между векторам 
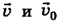. Величина вектора скорости 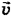при неизменных 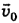и 
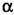будет изменяться только с изменением величины вектора 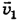, ведь вектор 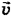равен векторной сумме векторов 
:
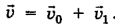
Модуль вектора численно равен длине штрихового отрезка, замыкающего на рис. 4-9 концы векторов . В каком случае длина этого отрезка будет минимальной? Очевидно, когда этот штриховой отрезок, а следовательно, и вектор 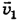будет перпендикулярен вектору 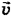, ведь длина перпендикуляра есть кратчайшее расстояние от конца вектора 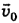до вектора .
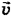Таким образом, скорость лодки относительно воды будет минимальна, когда вектор этой скорости направлен перпендикулярно вектору скорости лодки относительно берега (при неизменных остальных величинах, о которых говорится в условии задачи). Теперь, чтобы решить задачу, достаточно выразить искомую скорость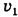 
через известную скорость течения 
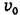и угол 
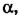, а неизвестный угол 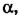в свою очередь выразить через известные ширину реки Н и расстояние Z, на которое снесет лодку вниз по течению. Из прямоугольного треугольника, образованного векторами 
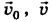и штриховой линией, равной модулю вектора искомой скорости 
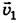, имеем:
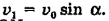
Из треугольника MON
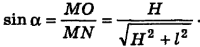
Подставив (2) в (1), мы решим задачу в общем виде:
Задача решена.
Ответ: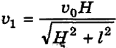 
.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
