Оглавление:
Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Пусть заданы две плоскости 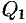 и
и 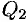 :
:
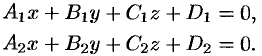
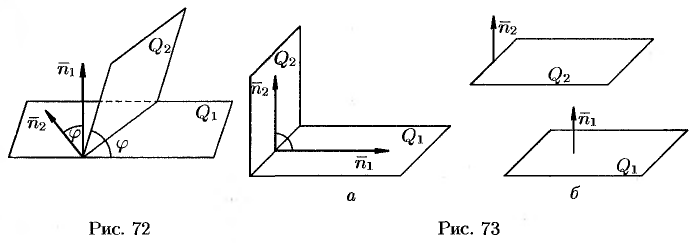
Под углом между плоскостями 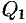 и
и 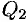 понимается один из двугранных углов, образованных этими плоскостями.
понимается один из двугранных углов, образованных этими плоскостями.
Угол 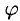 между нормальными векторами
между нормальными векторами 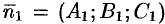 и
и 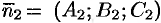 плоскостей
плоскостей 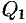 и
и 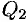 равен одному из этих углов (см. рис. 72). Поэтому
равен одному из этих углов (см. рис. 72). Поэтому 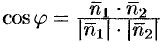 или
или
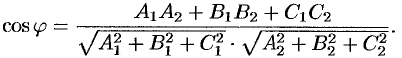
Для нахождения острого угла следует взять модуль правой части.
Если плоскости 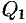 и
и 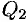 перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е.
перпендикулярны (см. рис. 73, а), то таковы же их нормали, т. е. 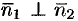 (и наоборот). Но тогда
(и наоборот). Но тогда 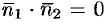 ,
,
т. е. 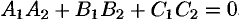 . Полученное равенство есть условие перпендикулярности двух плоскостей
. Полученное равенство есть условие перпендикулярности двух плоскостей 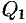 и
и 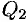 .
.
Если плоскости 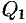 и
и 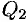 параллельны (см. рис. 73, б), то будут параллельны и их нормали
параллельны (см. рис. 73, б), то будут параллельны и их нормали 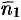 и
и 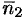 (и наоборот). Но тогда, как известно, координаты векторов пропорциональны:
(и наоборот). Но тогда, как известно, координаты векторов пропорциональны: 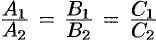 . Это и есть условие параллельности двух плоскостей
. Это и есть условие параллельности двух плоскостей 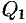 и
и 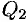 .
.
Расстояние от точки до плоскости
Пусть задана точка 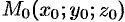 и плоскость
и плоскость 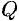 своим уравнением
своим уравнением 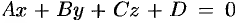 . Расстояние
. Расстояние 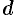 от точки
от точки 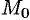 до плоскости
до плоскости 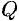 находится по формуле
находится по формуле
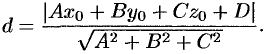
Вывод этой формулы такой же, как вывод формулы расстояния от точки 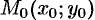 до прямой
до прямой 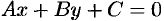 (см. с. 73).
(см. с. 73).
Расстояние 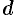 от точки
от точки 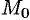 до плоскости
до плоскости 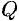 равно модулю проекции вектора
равно модулю проекции вектора 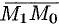 , где
, где 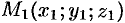 — произвольная точка плоскости
— произвольная точка плоскости 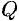 , на направление нормального вектора
, на направление нормального вектора 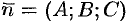 (см. рис. 74). Следовательно,
(см. рис. 74). Следовательно,
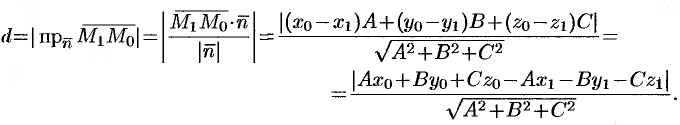
А так как точка 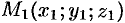 принадлежит плоскости
принадлежит плоскости 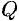 , то
, то
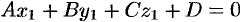 , т. e.
, т. e. 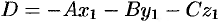 .
.
Поэтому 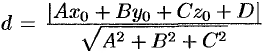 . Отметим, что если плоскость
. Отметим, что если плоскость 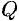 задана уравнением
задана уравнением 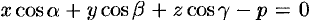 , то расстояние от точки
, то расстояние от точки 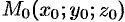 до плоскости
до плоскости 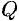 может быть найдено по формуле
может быть найдено по формуле
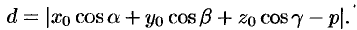
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Парабола |
| Общее уравнение линий второго порядка |
| Уравнения прямой в пространстве |
| Прямая линия в пространстве |

