Оглавление:
Плоскость и прямая в пространстве
Декартовой прямоугольной системой координат в пространстве называют совокупность трех взаимно перпендикулярных прямых пространства, пересекающихся в одной точке, на каждом из которых заданы положительные направления и единицы масштаба.
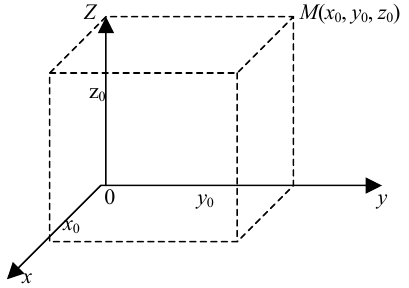
Прямые системы называются осями абсцисс, ординат и апликат. Положение любой точки пространства характеризуется тремя числами — координатами этой точки.
Рассмотрим уравнение плоскости и прямой в пространстве. Пусть 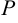 — произвольная плоскость в пространстве. Вектор
— произвольная плоскость в пространстве. Вектор 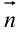 , перпендикулярный плоскости
, перпендикулярный плоскости 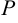 , называется вектором нормали к этой плоскости.
, называется вектором нормали к этой плоскости.
Если известна точка 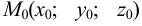 плоскости
плоскости 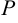 и
и 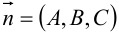 — вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена. Возьмем на плоскости
— вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена. Возьмем на плоскости 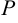 произвольную точку
произвольную точку 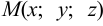 . Эта точка принадлежит плоскости
. Эта точка принадлежит плоскости  в том и только том случае, если вектор
в том и только том случае, если вектор 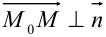 . Значит их скалярное произведение
. Значит их скалярное произведение 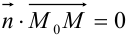 . Так как
. Так как 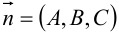 и
и 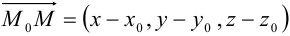 , то
, то 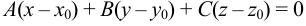 или
или
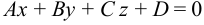 — уравнение плоскости в пространстве, где
— уравнение плоскости в пространстве, где 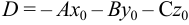 .
.
Всякую прямую в пространстве можно рассматривать как пересечение двух плоскостей, поэтому прямая в пространстве всегда задается системой уравнений двух плоскостей:
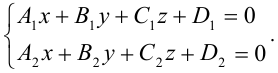
Направляющим вектором прямой в пространстве называют любой ненулевой вектор параллельный этой прямой. Если направляющий вектор прямой имеет вид 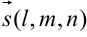 и точка
и точка 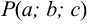 принадлежит данной прямой, то уравнение этой прямой записывается в виде
принадлежит данной прямой, то уравнение этой прямой записывается в виде
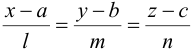 — канонические уравнения прямой.
— канонические уравнения прямой.
В частности, если известны две точки прямой в пространстве 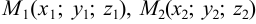 , то в качестве направляющего вектора этой прямой можно рассматривать вектор
, то в качестве направляющего вектора этой прямой можно рассматривать вектор 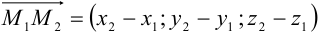 и уравнение прямой будет иметь вид:
и уравнение прямой будет иметь вид:
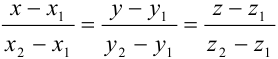 — уравнение прямой, проходящей через две заданные точки.
— уравнение прямой, проходящей через две заданные точки.
Уравнение прямой, проходящей через точку 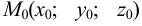 в заданном направлении
в заданном направлении 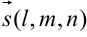 запишем в виде
запишем в виде
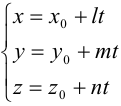 — параметрическое уравнение прямой.
— параметрическое уравнение прямой.
Задача №21.
Составить каноническое и параметрическое уравнения прямой, проходящей через точку 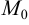 (l; -2; 3) и параллельно вектору
(l; -2; 3) и параллельно вектору  (2; 4;-5).
(2; 4;-5).
Решение:
Так как прямая параллельна вектору  , то координаты направляющего вектора прямой совпадают с координатами данного вектора, т. е.
, то координаты направляющего вектора прямой совпадают с координатами данного вектора, т. е. 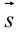 (2; 4;-5). Учитывая, что эта прямая проходит через точку
(2; 4;-5). Учитывая, что эта прямая проходит через точку 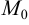 (1; -2; 3), запишем ее каноническое уравнение
(1; -2; 3), запишем ее каноническое уравнение
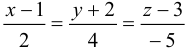
и параметрическое уравнение прямой
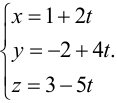
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Решение задачи на треугольник |
| Векторы и операции над ними задачи с решением |
| Скалярное, векторное и смешанное произведения векторов задачи с решением |
| Кривые линии второго порядка задачи с решением |

