Плоскость и поверхность

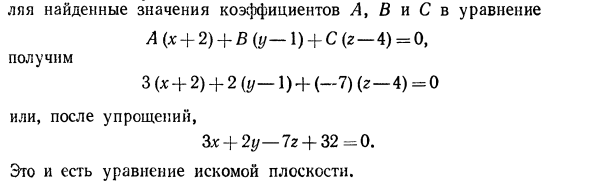
Плоскость

• плоскость /. Уравнение поверхности Как мы видели в гл. I, § 5, уравнение F (х, у) = 0, вообще говоря, определяет на плоскости некоторую линию, т. Е. Геометрическое место точек плоскости Оху, координаты которых х и у удовлетворяют этому уравнению. Подобно это уравнение F (х, у, z) = 0, вообще говоря, определяет в пространстве Охуга некоторой поверхности, т. е. геометрическое место точек, координаты которых х, у, г удовлетворяют уравнению F (х, у, г) = 0. Уравнение (1) называется уравнение этой поверхность, а х, у и г — текущими координатами.

В этом случае требуется найти уравнение поверхность, исходя из ее геометрических свойств. Найти уравнение шаровой поверхности (сферы) радиуса R с центром в точке Ох (хг; ух \ zx). (1) В соответствии с определенными сферами, расстояние между ее точками М (х \ у; z) от центра Огнях 3 (2) OtM = V (x-xty + (у-уг) ш + (г-гху (см. гл. I, формула (6)). Следовательно, У (х-хгу + {у-ухУ + (z-zxy = Ry или (х-хху + (у-угУ + (z-zxy = RK

Часто, однако, поверхность задается не уравнение, а как геометрическое место точек, обладающий тем или иное свойство. Людмила Фирмаль

сти Ах + Ву + Cz + D = 0, достаточно задать произвольно значения двух координат, а третью найти из уравнения плоскости. Проще всего определять точки пересечения плоскости с осями координат. Пример 1. Построить плоскость 2х — [- 3у 6z-6-0. Решение. Найдем точки пересечения плоскости с осями координат.

Для того чтобы найти точку пересечения плоскости с осью Ох, надо в уравнении плоскости при- Рис. 83 нять у-0 и 2 = 0 (так как для лмбой точки оси Ох у = Z— 0) .Имеем: 2л: -ЬЗ-О + б-0-6 = 0, откуда х ^ З. Аналогично, полагая х = 0, (/ = 0, н ю 2 • 0 -f 3 • 0 6 z-6 = 0, откуда г-1. Наконец, при л: = г = 0 находим у = 2. Итак, имеется плоскость 2х — \ — З 6г — 6 точки Mj (3; 0; 0), М, (0; 0; 1), Мг (0; 2; 0) (рис. 83).

• Решение задач по высшей математике

Матрицы и действия над ними	Прямая в пространстве
Линейные отображения	Прямая и плоскость в пространстве

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• … Пример 2. Построить плоскость 2х — \ — на — 10 = 0. Решение ЭТА Плоскость параллельна ОСИ Ог Для её построения ДОСТАТОЧНО найти ТОЧКИ Пересечения с осями Ох и Оу Полагая Л «= 0, найдем у = 2, полагая у — 0, найдем х = 5. Следовательно, плоскость проходит через точки Mj (0; 2; 0), М2 (5; 0; 0) (рис. 84). 5, Угол между плоскостями. Рассмотрим две плоскости и Q2, заданные соответственно уравнения: Atx + Bj_y + Clz + Dl = * 0 (плоскость Qv) и Azx ​​+ Вгу + Сгг — \ — Dt = 0 (плоскость Q2).

(рис. 85). Угол ф между нормальными векторами Nt и N2, Ql и плоскостей Q2 очевидно равен одному из указанных смежных двугранных углов (рис. 85). Поэтому Н.-Н * С05 <р == ПмТО (см. гл. III, формула (71)). Рис. 84 Рис. 85

Под углом между двумя плоскостями мы понимаем один из двугранных углов, образованных этими плоскостями Людмила Фирмаль

Иж-ЛЖ1 + BJ + Ctk, N2 = ^ .2i + B2j + C2k, то cos ср =,> M, + BA + CiC, (7) V ^ + FiJ + CJ-K ^ + Bi + C! Пример 1. Определить угол между плоскостями х — \ — 2у-3z-b4 = 0 и 2х + Зу + г + г = 0. Решение. Применяя формулу (7), получим 1.24-2.34-Г — ЗЫ 5 Итак, один из смежных двугранных углов приближается к равенству 69 ° 05 ‘. Рассмотрим теперь условия параллельности и перпендикулярности двух плоскостей. . Условие параллельности двух плоскостей Две плоскости Qj и Q2 тогда и только тогда параллельны друг другу, когда их нормальные векторы Nj = Л1 | -f- Вг) + С, к и N2 = Л21 — £ Вг) -f С2к параллельны между собой. Поэтому из условий параллельности двух векторов (см. Гл. III, формула (64)) получим __ (ял Аг ~ В2-С2 ‘W Это и есть условие параллельности двух плоскостей.

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих текущих координатах пропорциональны. Условие перпендикулярности. Две плоскости перпендикулярны друг другу тогда и только тогда, когда их нормальные векторы N, N-2 и взаимно перпендикулярны. Поэтому, воспользовавшись условием перпендикулярности двух векторов (см. Гл. III, ({юр-мула (69)), получим М. + ЯА + СА-О. (9) Равенство «(9) дает условие перпендикулярности двух плоскостей. Итак, две плоскости перпендикулярны друг другу тогда и только тогда, когда сумма парных произведений одноименных коэффициентов при текущих координатах равна нулю.

Пример 2. Составить уравнение плоскости, проходящей через точку М1 (-2; 1; 4) плоскими7-7-8 Наполнение уравнений связывания плоскостей, проходящих через точку Мх (—2; 1; 4) (см. Формулу (4)): А (х + 1) + С (г — 4) = 0. Нам нужно выделить ту, которая параллельна на плоскости Зх — \ — 2у — у тебя с азбука вием (8) параллельности плоскостей: —Итак, искомые коэффициенты Л, Б и С должны быть пропорциональными числами 3, 2 и —7.

в уравнениях L (х — \ — 2) — \ — В (у — 1) -fC (z-4) = О, получим 3 <* + 2) + 2 (у-1) + <-7) (г-4) = 0 или, после упрощений, Зх + 2у — 7z -f 32 = 0. Это и есть уравнение искомой плоскости. Пример 3. Через точку М1 (—2 \ 3; 6) провести плоскость перпендикулярно плоскостям 2х — \ — Зу — 2г — 4 = 0 и Зх + Заполнение уравнений связывания плоскостей, проходящих через точку М,: Л (x-f ~ 2) + £ ({/ -3) + С (г -6) = 0. Неизвестные коэффициенты А, В и С найдены из условий (9) перпендикулярности плоскостей: искомая плоскость должна быть перпендикулярной плоскостью 2х + 3у — 2г — 4 = 0, значит 2А + ЗЯ + (—.2) С = 0; искомая плоскость должна быть перпендикулярной плоскости 3 * + 50 + г = О, значит ЗА + 5-Я + 1 С ^ «0.

Итак, для нахождения неизвестных коэффициентов -0 ° j 2А -f ЗВ-2С-0, ЗЛ- | -5В -] — С Решая эту систему, найдем 3 -2 5 1 2 —2 3 1 2 3 3 5 -13k, B = —k Л -— 8к, С —к В частности, при / г = 1 найдем: Л = 13, В = —8, С-J. Подлежит найденным значениям Л, В и С в уравнении плоскости, проходящей через точку М ,, получм 13 (x-f2) — & (у— 3) -f 1 * (г-6) = 0 или 13л: -8y — \ — z — \ — 44 = 0. Точка пересечения трех плоскостей Пусть даны три плоскости Atx + Ba / — \ — C1z + D1 = 0, Atx + В, у — \ — + C2 * -fD2 = 0, А3х — \ — В3у + С.Лг -f- D3 = 0. Чтоти нужно точка пересечения этих плоскостей, нужно, очевидно, решить систему уравнений Af + Bty + Cf + D ^ 0, ‘Л ^ + Д ^ + С ^ + О.-О, Если определитель этой системы Л, Л, Ct Л., Вг С2 в, С, фо. А = То, что система имеет единственное решение. ** т. е. три плоскости пере-

Пример. х — \ — у-2г + 3 = 0, 2х — 2уЗг — 7-0; х + Зу — г-4 = 0. Решение. х + у — 2z + 3 ^ 0t ‘2х — 2у — \ — Зг —7 = 0, х4-3у — z — 4 = 0 ,, найденные координаты точки пересечения плоскостей: х = 1, х = 2; г = 3. Мы напучили искомое уравнение сферы, так как ему удовлетворяют координаты любой ее точки и, очевидно, не удовлетворяют координаты точек, не лежащих на данной сфере. В частности, если центр сферы находится в точке с координатами, то уравнение сферы (2) (3) х * + у * + г * = 1р.

Нормальный вектор плоскости. Уравнение плоскости, проходящей через точку Рассмотришь в пространстве плоскости В. Положение ее вполне определяется задание вектора N, перпендикулярный эта плоскость, и некоторая фиксированная точка Аи (jc4, ух \ г,), лежащий в плоскости Q. Вектор N, перпендикулярные плоскости Q, называется нормальный вектор этой плоскость. Если обозначить через А, В и С проекции нормального вектора N, то N = Л i + В j + Ck. Вывод уравнений уравнения плоскости Q, проходящей через точку точки Мх (jc1; у \ гх) и имеющей данные

Для этого рассмотрим вектор М, М, у соединяющей точки М, с произнесенной точкой М (х \ у; г) тл.сро При любом положении точки М на плоскости Q вектор МХМ перпендикулярна нормальный вектор N Q. плоскость Поэтому скалярное произведение ^^ — N = 0. Записает скалярное произведение МТМ * N через проекции. Так как МХМ = (х — хг) 1 — \ — (y — yx) \ — \ — (z-zl) kt вектор N = А \ + В \ — | -Ск, то (4) МХМ • N = Л (х-текст) + В (у-й) + С (z-zx) и, следовательно. Л (х — xj + В (у-ух) + С (z-г,) = 0.

. Мы показали, что координаты любой точки М (х \ у \ г) плоскость Q удовлетворяет уравнение (4) Нетрудно заметить, что координаты точек, не лежащая на плоскости Q, это уравнение не удовлетворяет (в последнем случае ЛШ | -Й # 0 ). Следовательно, нами получено искомое уравнение плоскости В. уравнение (4) называется уравнением плоскости, проходящей через данную точку.

Оно первой степени относительно текущих координат х, у и г. Мы показываем, что вся энергия соответствует уравнению первой степени относительной Пример 1. Написать уравнение плоскости, проходящей через точку М (\ — 2; 3) перпендикулярно вектору 2 Здесь А-2, В = О, С = 4. На основании формулы (4) получим 2 (х-.1) + О (0 + 2) + 4 (г-3) = О, или, после упрощения, х \ 2z-7 = 0.

Придавая коэффициентам А, В и С уравнения (4) различные значения, мы можем получить уравнение любой плоскости, проходящей через точку Мх (хх \ ух \ гх). Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей. Уравнение (4), коэффициенты Л, Б и С могут принимать любые значения, называемые уравнением связкисплс Пример 2. Составить урав— нить плоскости, проходящей через три точки Af, (л; -1; 0), Mt (2; 1; -3) и Л43 (-1; 0; 1) (рис. 82). м.

Напечатанное уравнение связки плоскостей, проходящих через точку м » ми A (x- ) + B (y + ) + Cz = 0. Так как векторы МХМ3 и МХМ3 лежит в искомой плоскости, то вектор, равные их векторное произведение и, следовательно, перпендикулярная эта плоскость, можно принять за ее нормальный вектор: я J K 1 2 —3 -2 1 1 N = МДх MtM3 = = 5i + 5j + 5k. Таким образом, Л = 5; # = 5; С = 5, и уравнение искомого при следующих просмотрах: 5 (* -1) + 5 (у -} — 1) + 5г = 0, или (/ + 2 = 0. 3. Общее уравнение плоскости и его частные случаи В п. 2 мы показали, что всякая плоскость соответствует уравнению первой степени относителоники Рассмотрим теперь общее уравнение первой степени с тремя переменными х, у иг. Лх + Б ^ -f Сг + 0 = 0. (5)

По крайней мере один из коэффициентов А, В или С не равен нулю, так как иначе мы имели бы не уравнение, а тождество D = 0. Предполагая для определенности, что Сф 0, представим уравнение (5) в виде А (х-0) + В (у-0) + С (г + = 0. (6) Уравнение (6) равносильно уравнению (5). Сравнивая уравнение (б) с уравнением (4), мы видим, что оно, а следовательно, и равносильное ему уравнение (5) являются уравнением плоскости

. Уравнением прямой, по которой наша плоскость пересекает координатную плоскость Оху Рекомендуем читателю установить, что плоскость Ах -} — Cz-ФД = 0 параллельна оси Оу, а плоскость К — \ — Cz — \ — {- £) = 0 параллельна оси. ох Итак, мы приходим к следующему выводу: если в уравнении плоскости отсутствует член, содержащий координату г или у, или ху то плоскость параллельна соответственно оси Oz или Оу, или ох. .

3. Коэффициент при текущей координате и свободный член равны нулю Например, C = D = 0. В этом случае уравнению Ах — {-. Ву = 0 соответствует плоскость, проходящая через начало координат (Согласно п. 1) Так как, кроме того , нормальный вектор плоскости