Плоскопараллельное движение твердого тела

Плоскопараллельное движение твердого тела

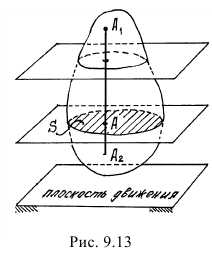
Плоскопараллельным движением называется такое движение, при котором все точки тела перемещаются в плоскостях, параллельных одной неподвижной плоскости. Называется эта плоскость плоскостью движения (рис. 9.13).

Все точки прямой 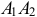, перпендикулярной этой плоскости, движутся одинаково, так как прямая перемещается поступательно. Поэтому для исследования движения всех точек тела достаточно определить движение только точек, расположенных в каком-нибудь сечении 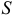, параллельном плоскости движения.

В дальнейшем на чертеже будем изображать лишь это сечение 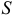, точки которого движутся в плоскости чертежа (рис. 9.14).

Положение сечения 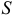и его точек будем определять в системе двух осе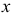й и .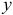

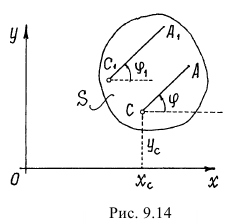
Это сечение 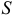при движении тела, перемещаясь по плоскости, ещё и поворачивается. Поэтому положение сечения будем определять с помощью координат 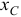и 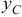какой-нибудь точки 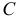(полюса) и углом 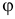между произвольно проведённой прямой 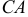и осью 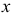(см. рис. 9.14).

Чтобы определить положение сечения 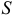и его точек в любой момент времени, достаточно задать функции времени

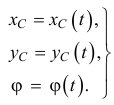
Эти функции называются уравнениями плоскопараллельного движения.

Конечно, если полюсом назвать другую точку, например 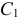, то первые два уравнения изменятся, так как точка 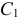движется иначе и по другой траектории.

А третье уравнение не зависит от выбора полюса. Действительно, если поворот тела определять углом 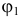между осью 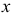и прямой 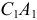, параллельной 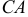, то углы будут всегда равны 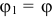и законы их изменения — одинаковы.

В качестве примера рассмотрим движение колеса, которое катится без скольжения по прямой (рис.9.15). Это движение будет плоскопараллельным, потому что все точки колеса движутся в одной вертикальной плоскости.

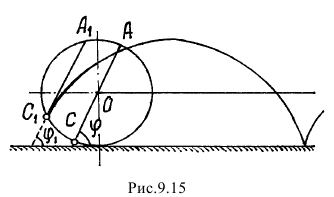
У полюса 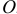, центра колеса, траектория — прямая. А у полюса 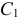траектория — циклоида. Уравнения движения этих двух точек разные. А углы 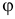и 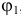, которые составляют диаметр 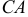, и хорда 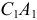, параллельная диаметру, с горизонтальной прямой всегда равны. Значит, и угловые скорост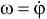и и 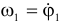, и угловые ускорения 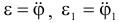, будут соответственно одинаковы.

Нетрудно заметить, что плоскопараллельное движение тела можно представить как сумму двух движений: движения полюса по некоторой траектории и вращения вокруг оси, проходящей через этот полюс перпендикулярно плоскости движения (вращения вокруг полюса).

Скорости точек тела. Мгновенный центр скоростей

Пусть известны уравнения плоскопараллельного движения

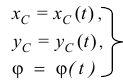
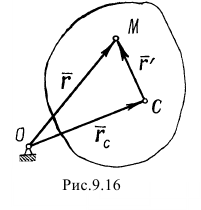
Найдём скорость какой-нибудь точки 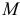(рис. 9.16).

Положение точки 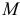определяется радиусом-вектором 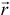, положение полюса 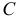— вектором 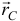. Проведём ещё один вектор 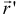из полюса 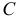в точку 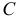. Тогда

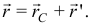
Скорость точки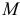

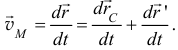
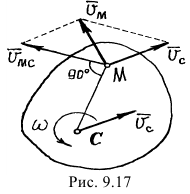
Первое слагаемое этой суммы равно скорости полюса 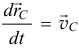(рис. 9.17).

Чтобы найти второе, условно остановим движение полюса, положим 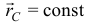. Тогда получим 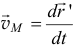. Значит, это второе слагаемое определяет скорость точки 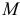при вращении тела вокруг как бы неподвижного полюса 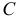и обозначается .

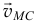Итак, скорость точки 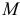тела есть векторная сумма скорости полюса и скорости точки при вращении тела вокруг полюса (рис. 9.17)

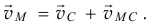
Скорость полюса можно определить, например, с помощью уравнений движения, с помощью производных 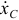и 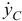(см.формулу 9.2). А скорость 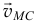— как скорость при вращении тела вокруг оси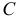

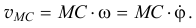
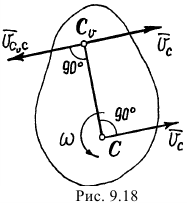
Найдём скорость ещё одной точки тела, точки 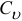, положение которой определяется как (рис. 9.18). Повернём вектор скорости полюса 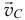на 90° по направлению угловой скорости 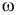. И в этом направлении отложим отрезок 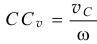. Скорость этой точки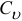

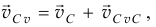
но

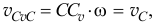
а вектор этой скорости 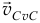перпендикулярен 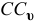и направлен в сторону, противоположную вектору 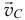. Значит, скорость точки 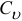как сумма векторов 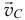и 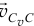будет равна нулю .

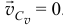Следовательно, при плоскопараллельном движении тела всегда можно найти такую точку, скорость которой в данный момент времени равна нулю. Эта точка 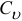называется мгновенным центром скоростей.

Положение этой точки на теле всё время меняется, так как скорость полюса в общем случае может изменяться и по величине, и по направлению; да и угловая скорость 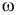также переменна.

Пусть положение мгновенного центра скоростей 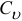известно (рис. 9.19). Назовем его полюсом. Тогда скорость точки 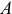по выражению (9.5)

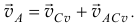
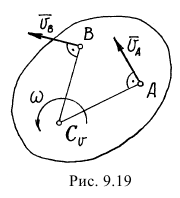
Но 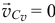. Значит, 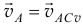и величина её

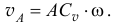
Аналогично скорость другой точки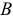

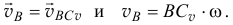
Следовательно, если известен мгновенный центр скоростей, то определение скоростей точек значительно упрощается. Предполагаем, что тело вращается вокруг оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения, и находим скорости при таком вращении.

Существует несколько способов определения положения мгновенного центра скоростей.

а) Если известны скорости двух точек тела, то мгновенный центр скоростей 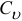находится как точка пересечения перпендикуляров к векторам этих скоростей, проведённых из данных точек (см. рис. 9.19).

При этом может оказаться, что точки расположены на одном перпендикуляре к скоростям (рис. 9.20). В этом случае надо искать 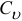как точку пересечения этого перпендикуляра с прямой, соединяющей концы векторов скоростей. Этот способ следует из того, что скорости пропорциональны расстояниям от точек до 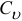и полученные треугольники подобны.

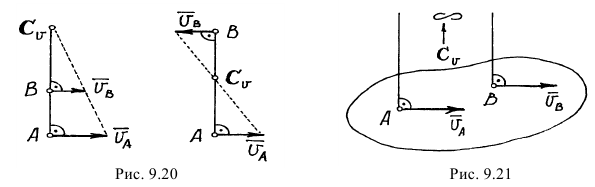
Может получиться и так, как показано на рис. 9.21. В этом случае мгновенный центр скоростей находится в бесконечности и угловая скорость 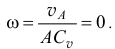. А при 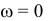как при поступательном движении скорости всех точек тела будут равны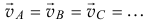

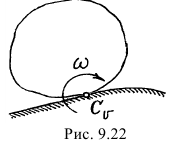
б) Если тело катится без скольжения по неподвижной поверхности (рис. 9.22), то мгновенный центр скоростей находится в точке касания, так как проскальзывания нет и скорости этой точки тела и поверхности в данный момент одинаковы, то есть равны нулю.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Вращение тела вокруг неподвижной оси

Вращение тела вокруг неподвижной точки

План скоростей

Ускорения точек тела. Мгновенный центр ускорений