Оглавление:


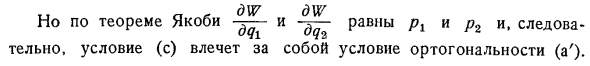

Плоское движение. Движение по поверхности. Общие положения
- Очевидно, что все вышесказанное относится к движению на плоскости или в более общих случаях, то есть на поверхности, когда вместо 3 используются 2 координаты qt и q2. Особенности н = к п = п + п. т я в зависимости от p2, qv q2 и t форма уравнения Якоби равна dV dV dV d p Полный Интеграл V qit q2, т. е.
Например, материальная точка может свободно описывать один и тот же эллипс под действием пяти следующих сил: притяжения, обратно пропорционального квадрату расстояния со стороны каждого из фокусов, притяжения, пропорционального расстоянию со стороны центра и, наконец, притяжений со стороны осей, обратно пропорциональных кубу расстояний. Людмила Фирмаль
если Av a известен для 2 произвольных констант ppa2, и ни одна из них не является аддитивной, то конечное уравнение движения имеет вид: дифференциальный клапан ПЛ дифференциальный клапан Точка Б. Если система координат qv q2 определяется независимо от времени, а функция U явно не зависит от времени, то время t не включается в коэффициенты уравнения J.
- Тогда вы можете поставить В = ГТ если W q2, a, d , где W qv q2, a, h полный Интеграл уравнения ДГ Л ч РЗ dq1 dq, ДЖО. Уравнение движения, используя не подводим постоянных выглядит так. Кроме того, первым из них является уравнение trajectory. In дополнение, dw dW П1 dqt пр йй а. Полученная траектория перпендикулярна кривой W = const.
В частности, таким путем можно, не изменяя движения, преобразовать кривую линию в прямую и свести задачу к вопросу прямолинейного движения. Людмила Фирмаль
Эта теорема может быть установлена путем вывода, согласующегося с вышеизложенным, о движении свободных точек. Скорость x , y t zr и смещение BX, Zd требования ортогональности. Би Джей, Уилл. Курсоры + г Зун г 82 = 0. ля. На поверхности в этом случае имеются = 7р и y = 71.2 = ж я, К2 Т….. икс 6Х Т =. Условие a может быть записано как: dq2 Или МН ч + Р2 2 = 0. Установить, что локус = а является ортогональной к кривой ля 91 2. Константа.
Достаточно указать, что скорость точки перпендикулярна смещению tyj, то есть смещению, заполняющему B 2, dlF dW, которое находится на этой кривой.
Смотрите также:
Решение задач по теоретической механике
| Геометрическое свойство траекторий | Параболическое движение тяжелой точки в пустоте |
| Декартовы координаты в пространстве | Центральная сила — функция расстояния |

