Оглавление:









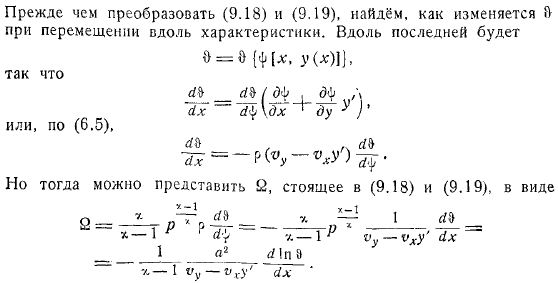
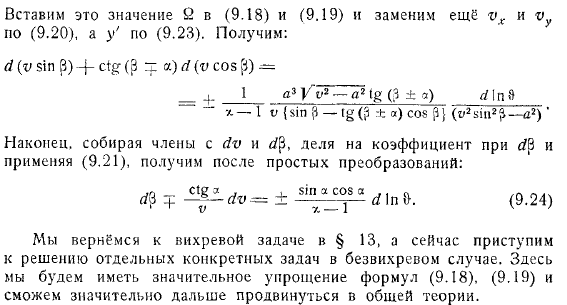

Плоские вихревые движения со сверхзвуковыми скоростями. Характеристики. Угол Маха
Исходя из этого, продолжим изучение дифференциальных уравнений движения. Есть конечных отношения. Уравнение Бернулли и условия термоизоляции.
И дифференциальных отношений решений задач по гидромеханике: вихревое представление. И уравнение неразрывности. Исключить плотность из непрерывности. Определение. Теперь, в виде, вы можете написать непрерывное уравнение, выражая o и отмечая его.
- Она формируется путем простого преобразования. Если выразить далее по формуле Бериулли и собрать термины в различные производные, то это будет выглядеть так.
- Обратите внимание, что он имеет одинаковую форму как в вихревом движении, так и без вихря.
Факт, когда вы заменяете выражение, вы получаете следующую форму. Людмила Фирмаль
Таким образом, это полностью выходит из уравнения. Напротив, уравнение указывает на наличие вихря.
Для большинства задач газовой динамики функция должна рассматриваться как известная функция. Если линии тока бесконечны (например, если поток трубки тока в сжимаемой жидкости вокруг контура неограничен), задача войдет в состояние, похожее на бесконечное. Если существует стационарное движение с бесконечным вихрем, равным нулю, то без сильного разрыва на пути движущейся частицы жидкости в этом движении она всюду находится в таком потоке.
- Когда частица проходит через поверхность с сильным разрывом, она изменяется с. Мы видели, что этот скачок вообще зависит от точки.
- Это заставляет общую теорию принять уравнение, правая сторона которого не равна нулю.
Я введу обозначения. Это написано как. Необходимо научиться решать дифференциальные уравнения вместе. К ним относятся неизвестные скорости и еще более неизвестные функции.
Однако эта функция включена только в и не находится под знаком. Людмила Фирмаль
To определите необходимость добавления. Начнем с теории простейшего случая соотношения. То есть предположим, что скорость движения во всех точках плоскости такова, что она превышает скорость звука, то есть во всех точках плоскости.
Наличие валидных характеристик позволяет разрабатывать эффективные методы решения системы. В случае плоской стационарной задачи предполагается, что кривая с уравнением строит характеристику, которая явно представляет собой линию, пересекающую плоскость цилиндрической поверхности. Это движение имеет свои особенности.
Показать производную. Добавить через, вдоль линии, по системе отношений, идущих вдоль. Опишите условие, что существует характеристика, то есть условие, что производные системы уравнений уравнений не могут быть четко определены.
Если вы представляете их и вставляете, это выглядит так. Поэтому вам нужно быть рядом. И затем. Во-первых, раскрыть детерминанты ваших следующих отношений, получив ссылку.
Отметим, что эта связь была получена уже в различных формах в общей теории слабых. Фактически получается, что проекция скорости газа на нормальность характеристической поверхности должна быть равна локальной скорости звука. Поэтому условие принимает следующий вид.
Чтобы было легче видеть, матч. Таким образом, наклон характеристики может принимать значения, которые определяются как корни уравнения порядка. Таким образом, вы можете нарисовать характерных элемента через каждую точку плоскости и покрыть всю плоскость (предполагая сверхзвуковое везде) с характерными семействами.
Если движение уже известно, то есть известно как координатная функция, то уравнение представляет собой дифференциальных уравнения, когда каждое интегрировано, оно дает систему характеристик в виде. Будущим мы всегда будем называть характеристику, ту, что соответствует знаку плюс перед корнем с. Ту, что в первом семействе, ту, что дает знак минус перед корнем.
Я буду писать соответственно. Однако плоские безвихревые движения он превращается в уравнение, которое должно выполняться по характеристике вдоль уравнения. Когда вы открываете и группируете участников, вы получаете первый. Или, в зависимости от расположения, разделить и заменить термином в квадратных скобках в правой части по формуле.
Здесь знак минус справа соответствует первому семейству, а вместо него надо стоять, а знак плюс соответствует значению. Произведение корней выражения можно выразить в следующем виде. Поэтому в соответствии с характеристиками первой семьи.
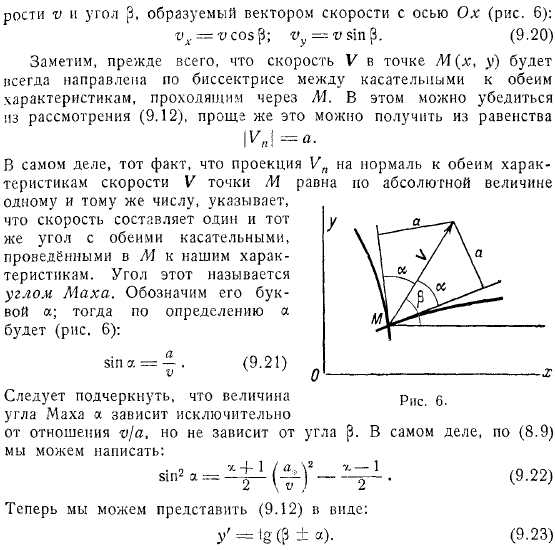
И вдоль вместо проекции скорости. Угол, образованный скоростью и вектором скорости с осями прежде всего заметим, что скорость точки всегда ориентирована вдоль биссектрисы между касательными обеих проходящих характеристик. Это видно из обзора, легче получить это из равенства.
В самом деле, тот факт, что проекция обеих характеристик скорости точки на нормальность равна одному и тому же числу по абсолютной величине, указывает на то, что скорость находится под тем же углом, что и обе касательные, втянутые в характеристику. Этот угол называется Маха. Обозначается буквой.
Следует подчеркнуть, что величина угла Маха зависит исключительно от него. Это зависит от отношения, но не от. Факт, вы можете написать.
Вы можете отобразить его в следующем формате. Перед преобразованием выясните, как он будет меняться при перемещении по характеристике. Вдоль последнего. Как это.
Но вы можете сделать это в следующем виде. Вставьте и замените это значение. Наконец, мы собираем термины, применяем их путем деления на коэффициенты и получаем после простого преобразования.
Вернитесь к вихревой задаче и начните решать отдельные специфические задачи при отсутствии вихрей. Здесь можно значительно упростить формулу и углубиться в общую теорию.

