Оглавление:


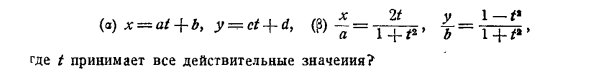
Плоские кривые
- Плоская кривая. До сих пор мы использовали обозначения для выражения функциональной зависимости y от x. .Y = / (*) • (1) Ясно, что это обозначение является оптимальным, если у определяется выражением с участием х. Однако функциональные зависимости, которые невозможно или неудобно выразить в этой форме, должны обрабатываться. Например, если y5-y- * = 0 или x * — \ — y * -ay = 0, мы знаем, что вы не можете явно выразить y как алгебраическую функцию от x. если x2 + y ° ‘+ 2Gx + 2Fy + C = 0t тогда y = -F-J- / H ^ x * -2Gjc-C;
- Однако функциональная зависимость y от x может быть легче выражена в исходном уравнении. Во всех этих случаях функциональную зависимость получают, делая функции двух переменных x и y равными нулю, т.е. уравнение f (xty) = 0. (2) Мы рассматриваем это уравнение как общее представление функциональных зависимостей. Поскольку y- / () — особый вид функции x и y, уравнение (1) включено в качестве специального случая. Таким образом, геометрическая позиция точки (, x, y) подчиняется уравнению f (x, y) = 0, графику, кривой или геометрической функции y, определенной уравнением / (x, y) = 0 Положение / (х, у) = 0 и для этой кривой или этого геометрического уравнения местоположения.
Существуют и другие способы представления кривых, но это часто полезно. Людмила Фирмаль
Предположим, что x и y являются функциями некоторой третьей переменной t, которая может иметь или не иметь геометрический смысл. Может записать X = / <), y = F (t). (3) Если конкретному значению присваивается t, соответствующие значения x и y известны.
| Графическое решение уравнений, содержащих одно неизвестное число | Геометрические места в пространстве |
| Функции двух переменных и их графическое представление | Смещения вдоль линий на плоскости |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Каждая пара таких значений определяет точку (x, y). Поэтому, если вы создадите все точки, соответствующие различным значениям tt, вы получите график геометрического положения, определенного уравнением (3). Например, x == a cos t} y = sin t, Изменить т от 0 до 27 г. Далее вы можете видеть, что точка (x: y) представляет собой круг с радиусом a, центрированным в начальной точке.
Если t принимает значение за пределами указанного диапазона, точка (x, y) повторяет один и тот же круг снова и снова. Исключение t дает π: 4- | — / = a2- обыкновенное уравнение окружности. Пример XVIII. 1. Пересечение двух кривых и уравнения f (xyy) -Oy cf (x, _y) = 0 (где / и <p — полиномы) определяется, если эти уравнения можно решить совместно для x и y.
Я могу Таким образом, два уравнения в принципе представляют собой конечное число изолированных точек. 2. Нарисуйте кривую (* -} — y) 2 = 1, xy = 1, x * -y1 = 1. 3. Уравнение f (x, y) — {- X <p (x, y) = 0 представляет собой кривую, которая проходит через пересечение кривых / = 0 и <p = 0. 4. Геометрические места, представленные уравнениями(а) X = al + b, y = ct + d, = *
Принимает все допустимые значения? Людмила Фирмаль

