Плоские кривые

Плоские кривые

Плоские кривые. Γ= {/*( / ); a == c 6} непрерывная дифференцируемая плоская кривая в плоскости xOy. И пусть 5 = 5 (P) переменная длина дуги кривой Γ.Получаем производные от выражений(16.13) и (16.14). Здесь, Если длина дуги 5(/)отсчитывается от начальной точки R (a) кривой, то берется знак»+», а если от конечной точки r (b), то берется знак» -«.Из уравнения дифференцирования дуги(16.20) следует уравнение Пусть точка(x(f0), y ((0)) не является сингулярной, то есть x ’°(10)+ y’1 (^0) 0, например x’(10) Φb. так как x ’(f0) 0, то и в окрестности точки находится x’(f) 0, то функция x (1) в этой окрестности возрастает строго монотонно.

То есть в окрестности неособой точки непрерывная дифференцируемая кривая является графом непрерывной дифференцируемой функции. Людмила Фирмаль

• Следовательно, существует обратная непрерывная дифференцируемая функция f = f (x). в представлении кривой Γ、 Точнее, существует непрерывная дифференцируемая функция y, определенная в окрестности точки 10 и в нескольких интервалах, включая точку x0 = x (^0).Следовательно, существует часть кривой, которая соответствует значению параметра, принадлежащего указанной окрестности точки / 0.График функции/.

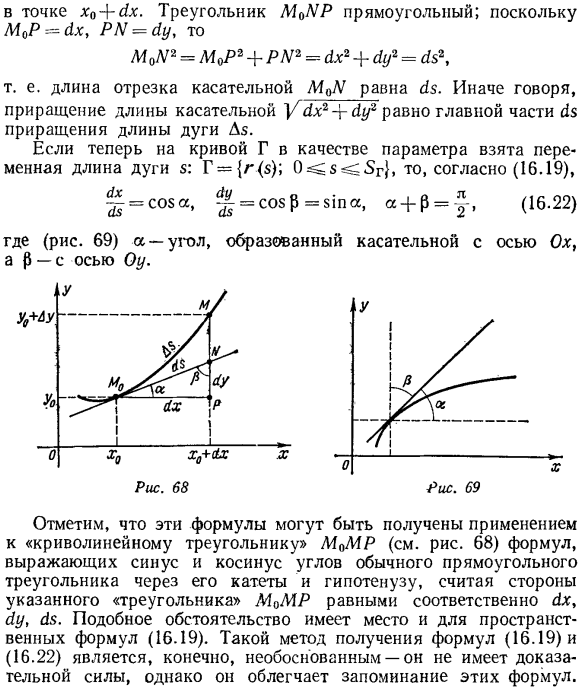
• И так оно и есть. Если кривая Γ является графом непрерывной дифференцируемой функции y = [(x), то формула (16.20) является формулой Если Γ-график непрерывной дифференцируемой функции y = [(x), afx^, а длина дуги кривой отсчитывается от начальной точки кривой(rps. Рассмотрим геометрический смысл формулы (68) (16.21).Позвольте мне. M0M-касательная в точке M0, pm = Ar / приращение функции в точке x0ph(1x, PM = yy-приращение ординаты касательной В точке x0 + c1x. МЫЫР треугольник, прямоугольник; M0P = УГ、 То есть длина касательного отрезка M0 M равна S.

То есть приращение длины касательной равно основной части приращения длины дуги. Людмила Фирмаль

• Здесь в качестве параметра кривой Г используется переменная длина дуги s. Р = {н-©;О^ З ^ 3Р}, то, согласно (16.19)、 Где (рис.69) a-угол, образованный касательной к оси Ox, а§ угол к оси Oy. Обратите внимание, что эти формулы получены путем их применения к»треугольнику кривой»М0МР (см. рисунок 68). ДЗ. Аналогичная ситуация наблюдается и в пространственной формуле (16.19).Таким образом, чтобы получить формулу (16.19) и (16.22), конечно, абсурдно-не стоит рассказывать, но это облегчит запоминание этих формул.

Смотрите также:

Предмет математический анализ

Касательная к кривой. Геометрический смысл производной вектор-функции.	Физический смысл производной вектор-функции.
Длина дуги кривой.	Две леммы. Радиальная и трансверсальная составляющие скорости.