Оглавление:







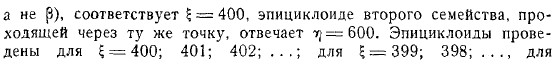


Плоские безвихревые движения
Если нет вихря, то есть. Уравнение может быть записано в соответствии с характеристиками первого семейства. В соответствии с характеристиками семейства. Кроме плоскости, в которой все покрыто характерными линиями, рассмотрим плоскость скорости.
Имеет дело со сверхзвуковыми скоростями решение задач по гидромеханике. То есть в этой плоскости необходимо учитывать точки, которые находятся вне окружности. С другой стороны, скорость газа. Таким образом, все точки интересующей плоскости располагаются в кольце между окружностями.
- Предположим, вы движетесь вдоль характеристики в плоскости. Мы двигаемся в самолете.
- Вообще говоря, по определенным направлениям. Эта линия называется первой семейной особенностью.
Эта строка, отношения должны быть заполнены везде. Людмила Фирмаль
Аналогичная конфигурация повторяется для характеристик семейства. Через точки на плоскости нарисуйте элементы характеристик семейств.
Пусть точка соответствует точке на плоскости (координаты точки являются компонентами скорости в этой точке). Тогда уравнение указывает, что касательная характеристики первого семейства, проходящая через плоскость, перпендикулярна характеристике второго семейства, проходящей через угол Маха соответствующую точку в плоскости (ось параллельна оси). Также касательная к характеристике семейства параллельна норме характеристики семейства.
- Характеристики в плоскости имеют различные формы в диффузионной задаче газовой динамики.
- Напротив, свойства плоскости всегда одинаковы для всех невращательных задач, поэтому их можно вычислить только один раз. Действительно, от равенства, например.
То есть необходимо определить свойства первого семейства плоскостей по обыкновенным дифференциальным уравнениям, так как они выражаются только с правой стороны, поэтому они не зависят от них явно, а только зависят от них. Для закрепления этого уравнения удобно направить плоскость в полярные координаты, уже введенные в. Другими словами, это просто случай без вращения.
А так как она зависит исключительно от отношения (точнее она зависит от отношения, поэтому переменная отделяется и достаточно выполнить квадратуру). Людмила Фирмаль
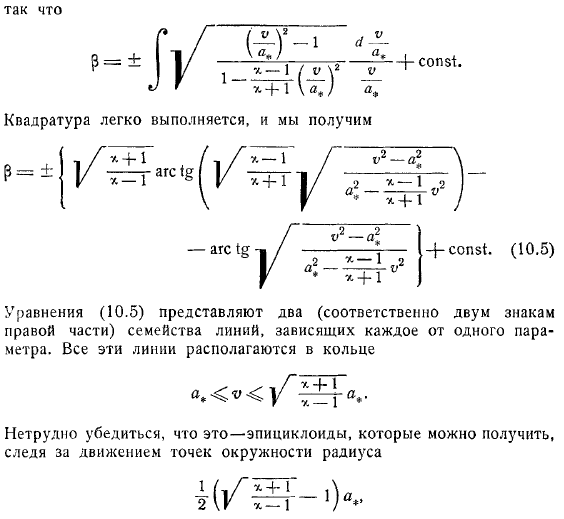
Как это. Квадрат прост и выглядит так.
Уравнение представляет собой семейство из строк (каждая с знаками справа), каждая из которых зависит от параметра. Все эти линии находятся в кольце. Легко проверить, что это эпициклоиды.
Это можно получить, наблюдая за движением точек окружности радиуса. Важно знать, на сколько вы готовы. В случае задач без вихрей характеристики плоскости всегда отображаются в виде эпициклоидов.
Вместо того, чтобы вводить угол, вы также можете записать равенство следующим образом. Для удобства дальнейших расчетов напишите характеристику первого семейства. С первым семейством эпизикоидов, проходящих через каждую точку плоскости (в кольце).
Второй. В этом случае разность значений соответствующих констант будет точно равна полярному углу точки. То есть он хранится по всему проходящему радиус-вектору, а сумма значений равна. Где находятся константы.
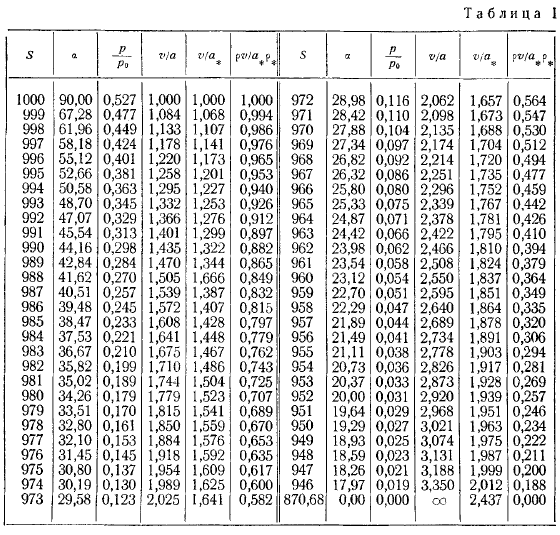
То есть он остается во всем круге с центром ведущим (проходящим через него). В прилагаемой таблице укажите количество и величину значений соответствующих значений а, начиная снизу. В плоскости направление обеих характеристик, проходящих через точку, может быть распознано уравнением, если они известны в этой точке.
Однако, если эпициклон уже подготовлен, то вы знаете, что вы можете найти направление без выполнения расчетов с помощью. Достаточно вспомнить, что элементы эпициклоиды, которые проходят (вместе с данными), перпендикулярны элементам противоположного ряда характеристик, которые проходят, например, таким образом, что необходимо провести линию перпендикулярно, чтобы построить направление первого признака семейства в какой-то точке. К касательной семейства, проходящей через эпициклоиду (ось всегда параллельна).
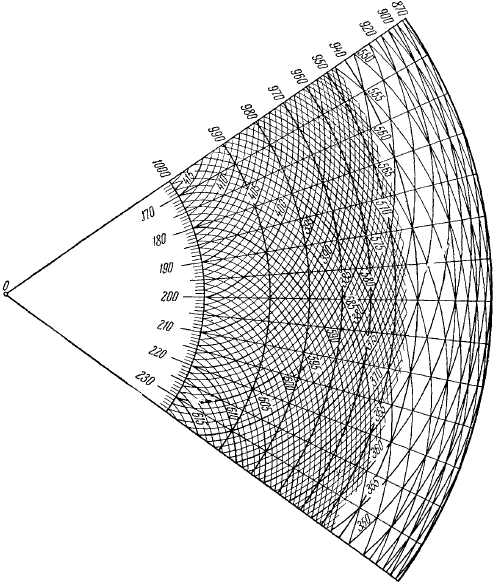
Показана часть использования характеристик для решения плоской безвихревой задачи плоскости (клин в окружности радиуса начала координат), на которой расположены часть эпизиоида групп и несколько окружностей. Вместо того, чтобы вводить цифры. В градусах новая константа является альтернативой.
Первое семейство эпизикроидов, проходящих через точку, не поддерживает семейство эпизикроидов, проходящих через ту же точку. Эпициклоидальный эффект Будьте осторожны во всех отношениях. Теперь мы покажем, как использовать характеристики для численного определения поля скорости и давления во всех точках плоскости в отдельных задачах газовой динамики.

