Плоская материальная кривая, уравнение которой, отнесенное к подвижной системе отсчета

Задача №10.

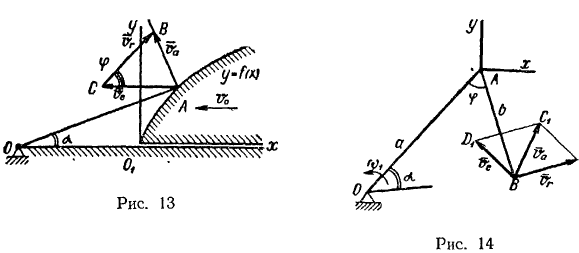
Плоская материальная кривая, уравнение которой, отнесенное к подвижной системе отсчета, имеет вид 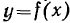, движется в своей плоскости поступательно справа налево с постоянной скоростью 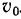. Палочка , длина которой равна 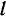, шарнирно закреплена одним концом в неподвижной точке 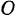и опирается на эту кривую другим (свободным) концом. Определить угловую скорость 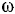палочки в зависимости от положения системы (рис. 13).

Решение:

Абсолютной траекторией точки является окружность с центром в точке 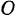. Вектор абсолютной скорости точки А направлен по касательной в этой окружности. Известно только направление этой скорости, по не величина. Свяжем подвижную систему отсчета с движущейся (кривой. Тогда переносное движение будет поступательным, а переносная скорость — скоростью 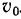. Относительное движение точки происходит по кривой 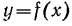, а потому и относительная скорость 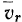направлена по касательной к этой кривой. Из 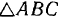имеем

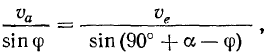
откуда имеем

Здесь

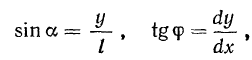
а потому

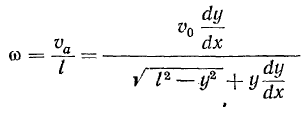
Условия постоянства скорости 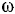получает вид

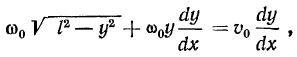
откуда

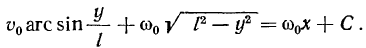
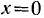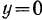Если же при имеем , то .

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №8. Точка описывает плоскую кривую. Радиальная составляющая скорости точки положительна и постоянна по величине, а радиальная составляющая ускорения отрицательна и обратно пропорциональна кубу расстояния от некоторого полюса. Определить траекторию и секторную скорость точки.

Задача №9. Пользуясь формулами для ускорения точки о полярной системе координат, доказать, что если ускорение точки равно нулю, точка будет совершать равномерное и прямолинейное движение.

Задача №11. Палочка длины а вращается в плоскости чертежа вокруг неподвижной точки с постоянной угловой скоростью (рис. 14). Вокруг подвижного конца этой палочки в той же плоскости вращается другая палочка длины так, что угол , заключенный между палочками, изменяется по закону где постоянна по величине. Определить абсолютную скорость точки , применяя теорему о сложении скоростей.

Задача №12. Лодку , уносимую течением реки, подтягивают веревкой к точке берега. Найти траекторию лодки, принимая последнюю за точку и считая, что скорость течения реки постоянна по всей ее ширине, скорость наматывания веревки постоянна по величине и равна и скорость лодки относительно реки все время направлена вдоль веревки (рис. 16).