Площадь поверхности вращения

Площадь поверхности вращения

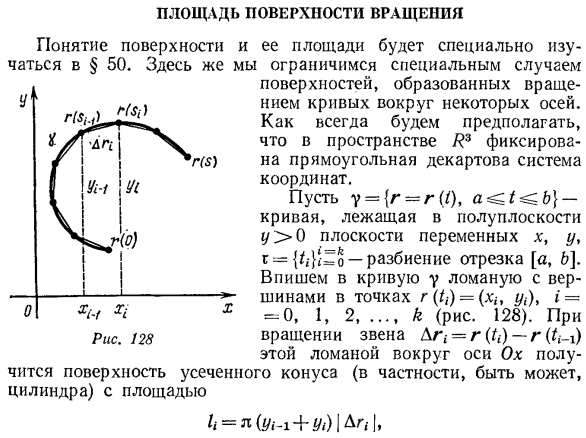
Площадь поверхности вращения. Понятие поверхности и ее площади специально изучено в§ 50.Здесь он ограничивается частными случаями. Поверхность, образованная вращением кривой вокруг определенного axis. As обычно, предположим, что ортогональная декартова система координат фиксирована в пространстве?3. пусть y = {r-r ({), a ^ 6} разбиение кривой, r = {^} = 0, и интервал[a, 6] в полуплоскости y 0 переменных x, y. на кривой y точка r(t)=(x;, y), I= 0,1, 2,…, напишите пунктирную линию с вершинами в k (рис. 128).

Если это пунктирное звено вращается вокруг оси Ox, мы получаем поверхность усеченного конуса с площадью (в частности, вероятно, цилиндр). Людмила Фирмаль

• Поверхности с площадью при вращении всей полилинии. Определение 1. Mn если есть ограничение на Lx, то оно будет называться Определяется площадь B поверхности, образованной вращением кривой y вокруг оси Ox. Подобный этому Теорема 4. пусть y = {r = r (((), и I 6} непрерывные производные Ступенчатой кривой без сингулярности в полуплоскости y-0 плоскости переменной x, y. тогда для площади поверхности L, полученной вращением кривой y вокруг оси x, уравнение.

Где in-переменная длина дуги кривой y, 0 ^ 5 ec5. Proof. As известно, что при допущениях, сделанных в теореме (см. раздел 16.5), функция b = 5 ((), a ^ 1 ^ b) является приемлемым преобразованием параметров, и поэтому длина дуги» » может быть использована в качестве параметра. m = {5r} 1 = 0 как разбиение интервала[0, 5]. Сравните количество Интегральная сумма (2pu функция ($）） Заметим, что для этой цели непрерывная функция y © на интервале[0, 5]является границей. То есть неравенство для всех 5 e [0, 5] / g /© / L4.

• Модуль непрерывности функции y (b) обозначается через ω (6; y), а длина пунктирной линии с вершиной в точке обозначается через kx Р(5р) и[Ар [^ДВ -, 1 = 1, 2, к Где: Fri(5-AT)= 0 (см. теорему 3), Fri u (bt, y)= 0 (см. Подразделы 19.6 удары 5 и 0 ^ Hm ^ 5.so Mn (ax-bx)= 0 Mnx =2π^ y (5) s, так что это также Mnx = 2nm (y) ys. By изготовление Помните, что в последнем Интеграле измените переменную 5 = 5 (I) и 55 = T / Gd ’ I. Где кривая y является явным уравнением y =?(X), если задано с помощью a ^ x ^ b, формула для площади поверхности, образованной вращением графика функции/вокруг оси Ox, имеет вид. Напомним, что (см. подраздел 16.4) VI + y ’ yx = ys, выражение (32.23),

Вывод предложенной формулы (32.20) имеет определенные недостатки, так как только в простейшем случае поверхности усеченного конуса и ее ассоциации понятие площади поверхности и ее аддитивности уже используется в этом выводе. Мы рассмотрим эти вопросы далее в разделе 50.5. Образцы. 1.Найти область 5 сферы с радиусом r. указанную сферу можно получить, вращая полукруг r / = V » r2-x2,-r ^ x ^ r вокруг оси Ox. Можно торговать.

Не используя понятие площади поверхности базовой поверхности, можно ввести общее понятие площади поверхности и приобрести необходимые свойства. Людмила Фирмаль

• Производная y ’ = ■ r x будет бесконечной в X =±г. Это гораздо удобнее взять параметрическое представление полукруга Тогда x ’= r zi (, y’ = rco5 /; таким образом, площадь поверхности 5 поверхности сферы с радиусом r можно легко вычислить по формуле(32.20). 2.Найти площадь 5 поверхности, образованной вращающейся вокруг оси Ox дугой цепной линии (см. Рисунок 107) y-acb〜、 -b ^ ^ x ^ ^ b(эта поверхность называется катеноидом).По формуле(32.23).

Смотрите также:

Предмет математический анализ

Объем тел вращения.	Работа силы.
Вычисление длины кривой.	Вычисление статических моментов и центра тяжести кривой.