Площадь криволинейной трапеции

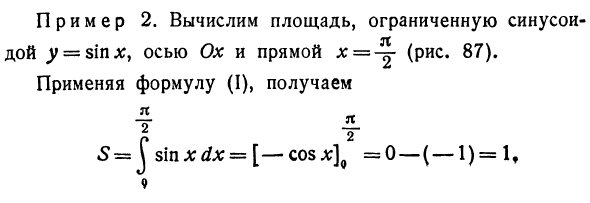
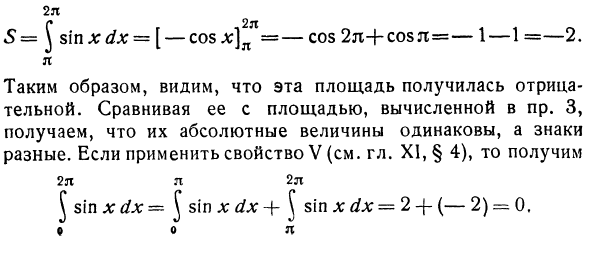
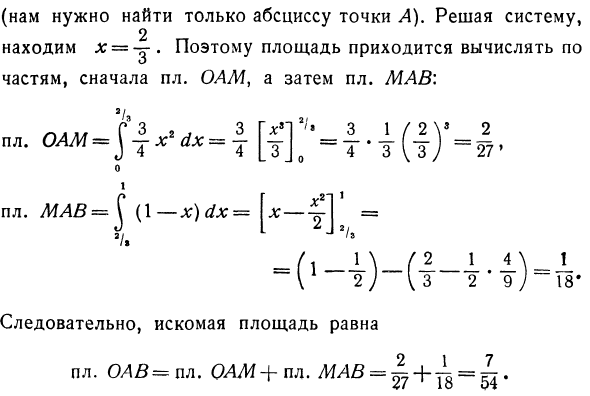
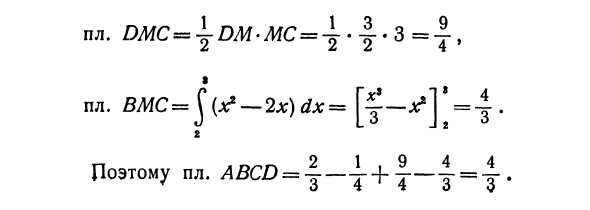
Площадь криволинейной трапеции

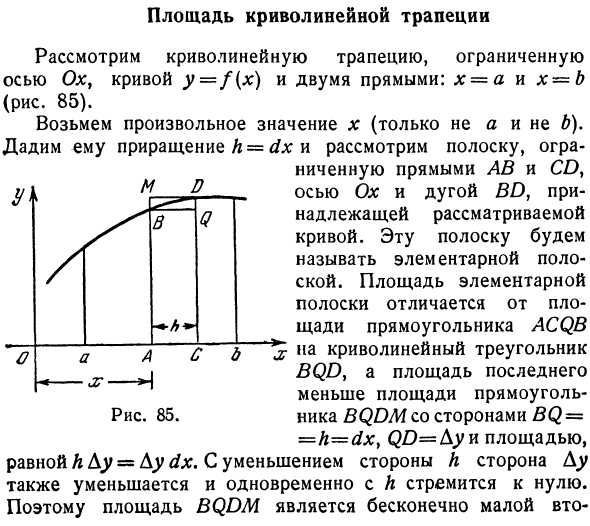
• Изогнутая трапециевидная зона Рассмотрим изогнутую трапецию, окруженную осью Ox, кривой y = f (x) и двумя прямыми линиями x = a и x-b (рис. 85). Принимает любое значение х (не а, не б). При заданном приращении h = dx рассмотрим полосу, окруженную прямой линией LP и CD, принадлежащей рассматриваемой кривой, оси Ox и дуге BD. Эта полоса называется базовой полосой.

Площадь элементарной полосы отличается от площади прямоугольника ACQB ^ изогнутым треугольником BQD, причем последняя область больше площади прямоугольника BQDM, равной сторонам £ Q = = h = dxf QD = A <y и h Ay = Aydx Это будет меньше. Когда сторона h уменьшается, сторона Du также уменьшается, и в то же время h стремится к нулю. Следовательно, область BQDM бесконечна Рисунок 85.

Роговый порядок. Площадь базовой полосы является приращением площади, а площадь прямоугольного ACQS является производной площади, равной LV-LS = / (x) dXy. Таким образом, сама область определяется путем интегрирования различий. . Пример 1. Рассчитайте площадь, ограниченную параболой y = 1 —x1 с прямыми линиями x = -, x = 1 и осью Ox (рис. 86). Рисунок 87. Где f (*) = 1-x * 9, пределы интеграции a = -and b = \, поэтому 5 = —х? ) Dx = y] ‘= 1 — 2 f_l_ ± f_ ± Yl__ ?? \ s; L 2 3V 2y J 3 24 24 * (О у = 7-х г Рисунок 86.

На рассматриваемом рисунке независимая переменная x изменяется от a к a, поэтому желаемая область S равна S = J / (х) дх Людмила Фирмаль

Пример 2. Рассчитать площадь, окруженную синусоидой y = * $ inx} с осью Ox и линией * = (рисунок 87). Используя формулу (I) T S = Jsin * dje = [-cosa:] 0 = 0 — (- l) = lf Пример 3. Вычислить площадь, окруженную дугой синусоиды y = sin xy, заключенной между двумя смежными пересечениями с осью Ox (например, между началом координат и точкой с абсциссой i). Обратите внимание, что из геометрических соображений ясно, что эта область в два раза больше, чем в предыдущем примере.

Но давайте сделаем расчет: я sinxdx = [-cosx] * = -cos i — (- cosO) = l + 1 = 2. о На самом деле наше предположение оказалось справедливым. Пример 4: Рассчитать площадь, окруженную синусоидой, ^ Осевая корова * Бунт (Рисунок 88). По предварительной цифре 88 можно судить Площадь пр. Предположим, 4 раза 2 Но после выполнения расчета, врач общей практики R G 12Я S = ^ sin xdx = [-cos x] Q = = –Cos2k — (- cosO) = -1 + 1 = 0 Этот результат требует объяснения.

• Чтобы выяснить природу проблемы, мы также вычислим площадь, окруженную той же синусоидой y = sin x и осью Ox в диапазоне 2π от z. Используйте уравнение (1) для получения:второй S2ji sin xdx = [-cosx] l-cos 2n + cosrc = -1—1 = –2. Я Таким образом, эта область была признана отрицательной. Пр это. По сравнению с площадью, рассчитанной в 3, вы можете видеть, что их абсолютные значения одинаковы, а знаки различны. Применяя свойство V (гл. XI, см. §4), получим 2π и 2π. J sin x dx к J sin l; dx -f- \ sin l; dx = 2 + (-2) = 0 9 0 л

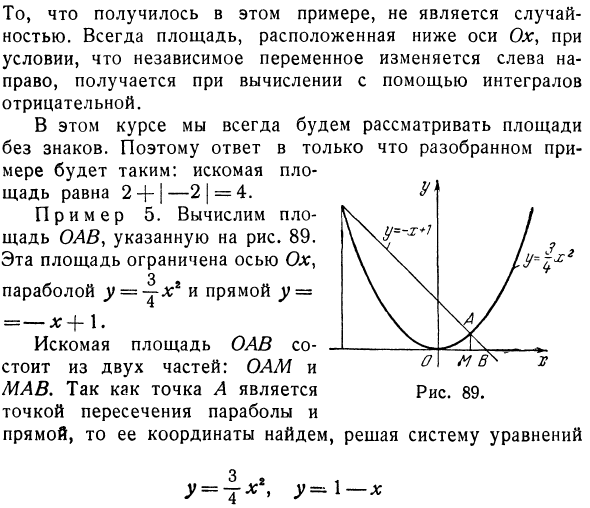
То, что произошло в этом примере, не случайно. Когда независимая переменная изменяется слева направо, отрицательный расчет путем интегрирования всегда получает область ниже оси Ox. Этот курс всегда рассматривает области без признаков. Поэтому ответ исследуемого примера таков: Целевая область 2 + | —2 |. = 4 Пример 5. Расчет площади автономной адресной книги, показанной на рисунке 89. Эта область ограничена осью 3 Парабола y = ~ xr и прямая y = = —X + 1. Требуемая область автономной адресной книги состоит из двух частей: OAM и MAV. Поскольку точка А является пересечением парабол, Линия, а затем ее координаты могут быть найдены путем решения системы уравнений 3 2 Y = T * ‘Y ^ 1 — x Рисунок 89.

(Вам нужно только найти абсциссу точки А). ОАМ и пл. MAS: 3 / Д з 2. 3 G * s «l 3 1/2 для 2 квадратных OAM = ^ x dx = j [TJ s (TJ = 27, о 1 ± 3 2 * 9 пл. = ^ (1 —x) dx = \ x— = 3 /, 2/8 Следовательно, целевая область пл. 0 / Ш = Квадрат ОЛЖ + пл = ^ +

Решение системы выглядит следующим образом = поэтому площадь сначала должна быть рассчитана в единицах pl. Людмила Фирмаль

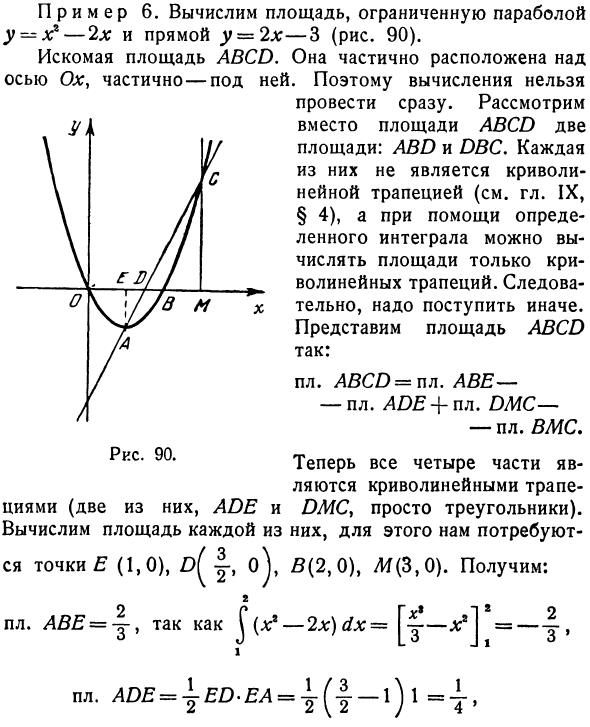
Пример б. Вычислите площадь, ограниченную параболой y = x2-2x и линиями y ~ 2x-3 (рисунок 90). Область поиска ABCD. Это частично выше и ниже оси ОК. Поэтому расчет невозможен Держи немедленно. Рассмотрим две области, ABD и DBC, а не область ABCD. Каждый из них не является изогнутой трапецией (см. Главу IX, § 4), и, используя определенный интеграл, вы можете рассчитать только площадь изогнутой трапеции.

Поэтому это должно быть сделано по-другому. Представьте себе область ABCD следующим образом: л / т \ \ \ ч . en / I 0 Vjу / в м 7A Рисунок 90 пл. ABCD = ID Abe-пл. ADE -f пл. DMC- -pl. военно-морской флот Теперь все четыре части — изогнутые трапеции (две из ADE и DMC, только треугольник). Рассчитайте каждую область. Точки: E (1.0), o), 5 (2.0) и M (3.0). Что получить: 2 пл. ABE = y, J (* ‘-2x) dx = [y-at’J «= — |, пл. ADE = ± ED-EA =пл. DMC = ^ DM-MC = * пл. BMC = ^ (x * -2x) dx 2 Следовательно, пл. ABCD = т

Смотрите также:

Предмет высшая математика

Свойства определенного интеграла	Объем тела вращения
Задачи на применение определенного интеграла	Объем тела, у которого известны площади поперечных сечений