Площадь криволинейной трапеции
Криволинейной трапецией называется плоская фигура в декартовой прямоугольной системе координат на плоскости, которая ограничена снизу осью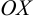 
, сверху графиком некоторой непрерывной функции 
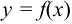, принимающей на отрезке 
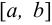только положительные значения, слева прямой 
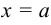, а справа прямой 
.
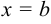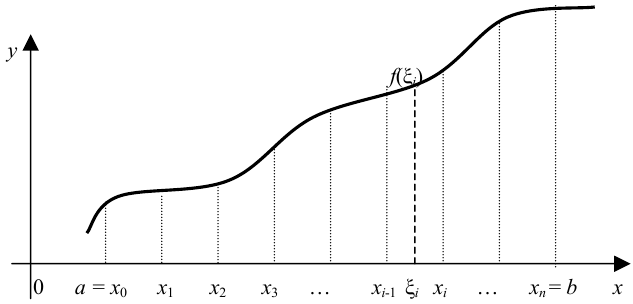
Поставим задачу вычислить площадь заданной криволинейной трапеции. Для этого отрезок 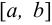разобьем точками 
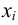на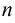 
равных частей.
В точке 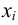восстановим перпендикуляр до пересечения с графиком функции. При этом криволинейная трапеция разобьется на 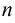малых криволинейных трапеций и 
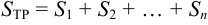. На каждом отрезке 
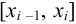выберем некоторую точку 
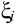. Этому значению 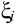соответствует некоторое значение функции 
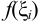. Рассмотрим прямоугольник с основанием 
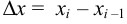и высотой 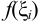. Его площадь 
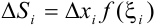. Можно считать, что 
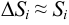и это приближение будет, очевидно, тем точнее, чем меньше будет величина 
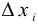. Поэтому естественно считать
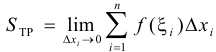
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
