Пластический изгиб статически определимой балки
Ограничимся рассмотрением малых упругопластических деформаций, когда деформации малы по сравнению с размерами элемента конструкции (теория Ильюшина). Рассмотрим статически определимую шарнирно опертую балку прямоугольного сечения.
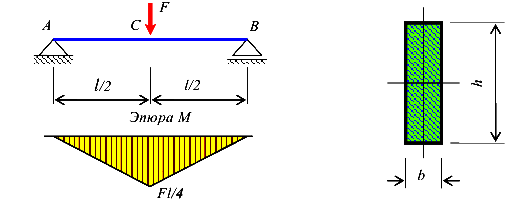
При увеличении силы F напряжения в крайних волокнах балки вначале достигают предела текучести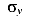 
(1я стадия). Однако несущая способность балки еще не исчерпана. Дальнейшее увеличение нагрузки вызывает распространение пластических деформаций в сторону нейтральной оси. При этом нейтральная ось все время остается центральной осью сечения (рис. 150).
Если пластические деформации распространяются на все сечение (2я стадия), то образуется пластический шарнир и несущая способность балки будет полностью исчерпана.
Пластический шарнир отличается от обычного шарнира тем, что он передает изгибающий момент равный пластическому моменту, а обычный шарнир вообще не передает момента. На первой стадии работы балки внешний и внутренний (изгибающий) моменты в поперечном сечении балки должны быть равны (561)
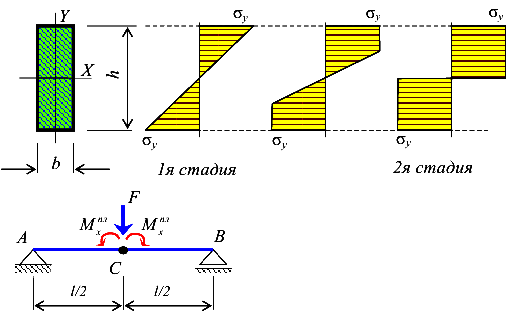
I я стадия
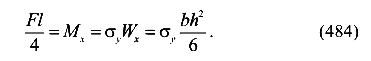
Определим соответствующую предельную силу для упругой балки
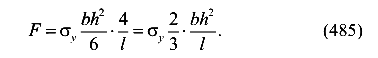
На второй стадии работы балки внешний и внутренний (изгибающий) моменты в поперечном сечении балки также должны быть равны друг другу (486)
2 я стадия.
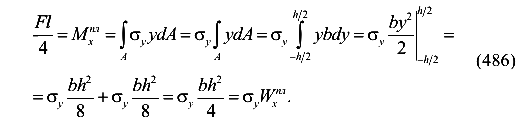
Предельная сила для балки с пластическим шарниром выражается формулой (487)
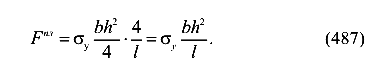
Отношение предельной силы для балки с пластическим шарниром к предельной силе для балки в упругой стадии равно
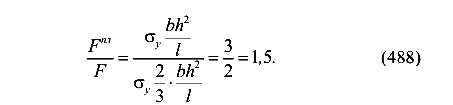
Упругий момент сопротивления прямоугольного сечения балки равен
Пластический момент сопротивления прямоугольного сечения балки, согласно выражению (486) равен
Пластический момент сопротивления сечения произвольной формы, согласно выражению (486), равен
где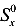 
— статический момент относительно нейтральной (центральной) оси части сечения, расположенной выше или ниже нейтральной оси.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Факторы, влияющие на величину предела выносливости |
| Учет пластических деформаций при расчете элементов |
| Изгиб прямых стержней |
| Типы опор и типы балок |
