План ускорений

План ускорений

• Предположим, что из плана ско­ростей известны скорости всех точек, принадлежащих телу BD (фиг. 48, а), и абсолютные ускорения ав н a D двух его точек В и D . Требуется определить ускорение ам точки М , принадлежа­щей телу BD . Тело BD совершает сложное дви­жение. Рассматривая его как движе­ние вместе с точкой В и вращение вокруг точки В, получаем для опреде­ления полного ускорения точки М векторное уравнение а м ~ а в + а мв или, так как полное относительное ускорение ам в является трической суммой

нормального и тангенциального, а в 4” а МВ 4′ а МВ’ В этом уравнении ускорение ав известно по величине и направ­лению, нормальное ускорение амв направлено от точки М к точке В геоме-36 Кинематический анализ плоских механизмов и равно Vmb : тангенциальное ускорение амв направлено перпендикулярно к ВМ , величина же его неизвестна. Рассматривая движение точки М как движение вместе с точкой D и движение относительно D, получаем а м ~ a D + + ^ M D , где aD известно по величине и направлению, амв = v2m d : 1M d и направлено по DM от М к D; aMD . Для определения

неизвестное по величине направ­лено перпендикулярно к DM Людмила Фирмаль

ускорения точки М аналогично плану скоростей можно построить план ускорений. Правая часть каждого из приведенных выше векторных урав­нений указывает, что ускорение ам может быть получено в резуль­тате геометрического сложения трех ускорений. Основываясь на первом из этих уравнений, проводим от произ­вольной точки тс (фиг. 48, б), которую в дальнейшем будем называть полюсом плана ускорений, вектор тсб первого из геометрических сла­гаемых — вектор ав . К концу этого вектора должен быть пристроен вектор Ьпм в второго геометрического слагаемого — ускорения амв

-На схеме тела ускорение амв направлено от точки М к точке В, поэтому и вектор Ьпм в от точки b должен быть направлен параллельно МВ вниз налево. Вектор Ьпм в должен быть отложен в таком же масштабе, в каком был отложен и вектор тсЬ. Масштаб плана ускорений, определившийся после проведения вектора тсб, равен < м/сек2 • мм и поэтому ЬпмМ Вв — вмм. V-a К концу вектора Ьпм в , т. е. к точке мы должны пристроить вектор последнего

• геометрического слагаемого — ускорения ахмв. Так как это ускорение известно только по направлению, то прихо­дится ограничиться проведением линии действия его перпендикулярно к МВ или, что одно и то же, перпендикулярно к Ьпм в . Таким образом, в результате использования первого из приведенных выше векторных уравнений выявляется лишь только то, что точка пг — конец вектора тст абсолютного ускорения ам этой точки — должна лежать на линии действия ускорения амв, проведенной через точку В соответствии со вторым из приведенных выше векторных урав­нений проводим из

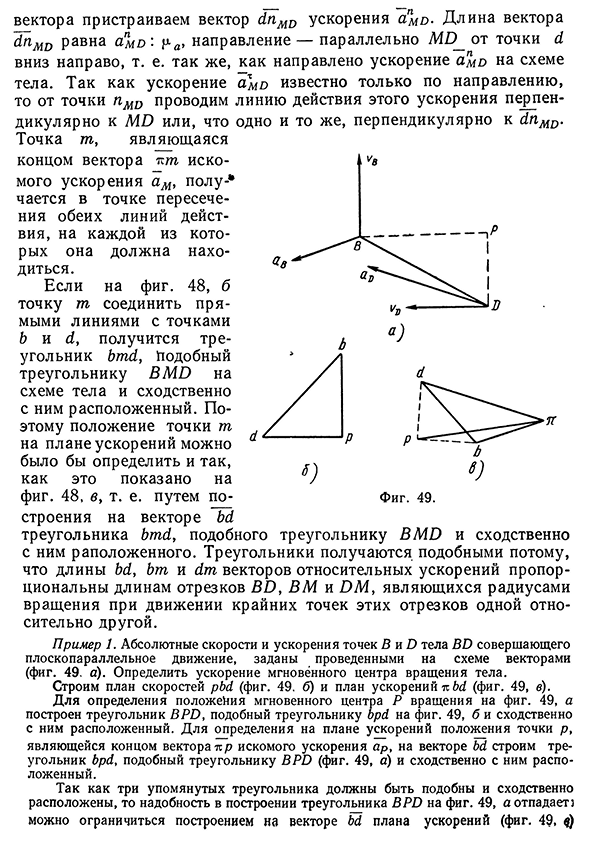
полюса тс вектор тсб/ ускорения aD, к концу этого План ускорений 37 вектора пристраиваем вектор dnMD ускорения clmdДлина вектора dnMD равна Omd : направление — параллельно MD__ от точки d вниз направо, т. е. так же, как направлено ускорение o,md на схеме тела. Так как ускорение aM D известно только по направлению, то от точки nMD проводим линию действия этого ускорения перпен­дикулярно к M D или, что одно и то же, перпендикулярно к dnM D . Точка тп, являющаяся концом вектора т иско­мого ускорения ам , получается в точке пересече­ния обеих линий дейст­вия, на каждой из кото­рых она должна нахо­диться. Если на фиг. 48, б точку т соединить

пря­мыми линиями с точками b и d, получится тре­угольник bmd, Подобный Людмила Фирмаль

треугольнику BM D на схеме тела и сходственно с ним расположенный. По­этому положение точки т на плане ускорений можно было бы определить и так, как это показано на фиг. 48, в, т. е. путем по­строения на векторе bd g) в) Фиг. 49. треугольника bmd, подобного треугольнику BM D и сходственно с ним раположенного. Треугольники получаются подобными потому, что длины bd, bm и dm векторов относительных ускорений пропор­циональны длинам отрезков B D , ВМ и D M , являющихся радиусами вращения при движении крайних точек этих отрезков одной отно­сительно другой. Пример 1. Абсолютные скорости и ускорения точек В n D тела BD совершающего плоскопараллельное движение, заданы

проведенными на схеме векторами (фиг. 49. а). Определить ускорение мгновённого центра вращения тела. Строим план скоростей pbd (фиг. 49, 6) и план ускорений те bd (фиг. 49, в). Для определения положения мгновенного центра Р вращения на фиг. 49, а построен треугольник B P D , подобный треугольнику bpd на фиг. 49, б и сходственно с ним расположенный. Для определения на плане ускорений положения точки р, являющейся концом вектора тер искомого ускорения аР , на векторе bd строим тре­угольник bpd, подобный треугольнику B P D (фиг. 49, а) и сходственно с ним распо­ложенный. Так как три упомянутых треугольника должны быть подобны и сходственно

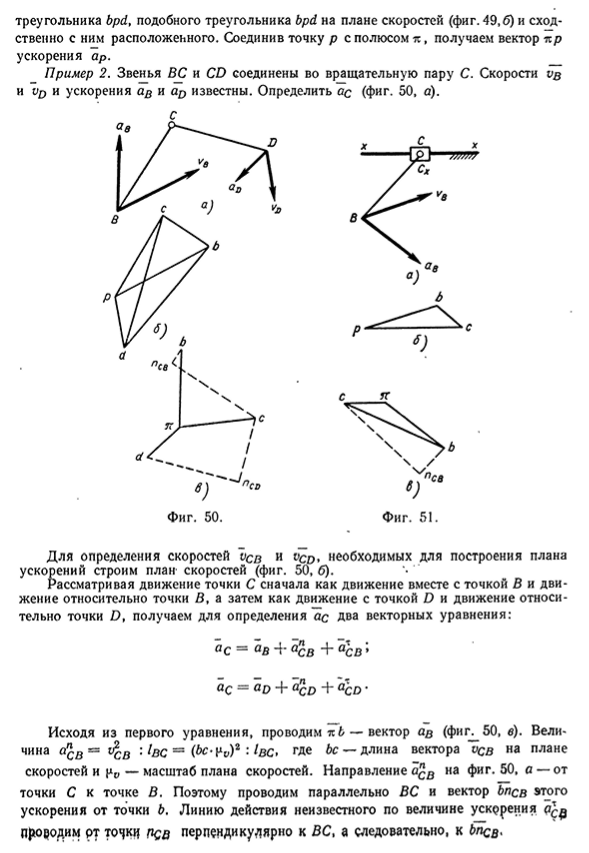
расположены, то надобность в построении треугольника B P D на фиг. 49, а отпадает] можно ограничиться построением на векторе bd плана ускорений (фиг. 49, $)38 Кинематический анализ плоских, механизмов треугольника bpd, подобного треугольника bpd на плане скоростей (фиг. 49,6) и сход­ственно с ним расположенного. Соединив точку р с полюсом к , получаем вектор тер ускорения ар. Пример 2. Звенья ВС и CD соединены во вращательную пару С. Скорости vq и t/p и ускорения ар и aD известны. Определить ас (фиг. 50, а). b Фиг. 51. Для определения скоростей асв и i>cd, необходимых для построения плана ускорений строим планскоростей (фиг. 50,6). Рассматривая движение точки С сначала как движение вместе с точкой В и дви­жение относительно точки В, а затем как движение с точкой D и движение

относи­тельно точки D, получаем для определения ас Два векторных уравнения: а с — ав + асв 4″ асв ’ а С — a D + a CD + a CD • Исходя из первого уравнения, проводим тс 6 — вектор «в (фиг. 50, в). Вели­чина = t^B 1вс — (bC’Pv)2 • 1вс> где Ъс — длина вектора vcb на плане скоростей и — масштаб плана скоростей. Направление а^в н а Фи г $0» а — о т точки С к точке В. Поэтому проводим параллельно ВС и вектор Ьпсв этого ускорения от точки Ь. Линию действия неизвестного по величине ускррения а ^ Проводим рт то^ки пев перпендикулярно к ВС, в следовательно, к Ьпсв<План ускорений 39 В соответствии со вторым уравнением проводим nd — вектор ар, затем из конца этого вектора dnc^ — вектор °со = VCD I cd= (cd-^v)2 ■ Icd параллельно CD вправо и из точки «с? линию действия axC D перпендикулярно к CD. Точкой пересечения линий действия

определяется величина и направление те с вектора «с-Пример 3. Звено ВС связано с ползуном, двигающимся по неподвижной направ­ляющей хх (фиг. 51, а) во вращательную пару С. В момент, соответствующий изобра­женному на фиг. 51, а положению, скорость vb и уско­рение ав известны. Определить ас-Сначала строим план скоростей, необходимый для построения плана ускорений (фиг. 51, б). Рассматривая сначала движение точки С как движе­ние вместе с точкой В и движение относительно точки В, а затем как движение вместе сточкой Сх , жестко связанной с направляющей, и движение относительно этой точки (точку Сх можно предположить находящейся на напра­вляющей под точкой С), получаем для определения ас два векторных уравнения: «С = а в -г* а с в + а св*’ «с

= а с х + a ccx + ахс с *. полюса л b ~ Vcb : lBC = (bc-^vY : 1В С, Основываясь на первом уравнении, проводим из вектор ов(фиг. 51, в). Величина а^в = где Ьс — длина вектора vqb на плане скоростей и — масштаб плана скоростей. Длина Ьпсв— Ос в : На, где Ьпсв — вектор ав в п ра — масштаб плана ускорений. Направление ав в на фиг. 51, а — от точки С к точке В, поэтому и на плане ускорений вектор Ьпсв проводим параллельно ВС от точки b вниз налево. Величина ахс в неизвестна, направ­ление перпендикулярно ВС, а следовательно, и Ьпсв ; в таком направлении и прово­дим от точки пев линию действия этого ускорения. В правой части второго уравнения первые два геометрических слагаемых равны каждое нулю: асх потому, что точка Сх неподвижна, а а^с = v2c c : р потому, что радиус р кривизны траектории, по которой точка С перемещается относительно точки

Сх , равен бесконечности. Ускорение ассх на фиг. 51, а направлено вдоль направляющей хх, поэтому из полюса те проводим линию действия этого ускорения параллельно направляющей. Точкой с пересечения линий действия а^в и Oqq определяется величина и на­правление те с — вектора Вектортесна плане ускорений направлен влево, а вектор рана плане скоростей— вправо; следовательно, точка С в положении, изображенном на фиг. 51, а, движется замедленно. Пример 4. Построить план ускорений для механизма, схема которого приведена на фиг. 52, а, При составлении векторных уравнений для определения ускорений &в необходимо принять во внимание, что точка В, перемещаясь по вращающемуся звену,40 Кинематический

анализ плоских механизмов движется с поворотным (кориолисовым) ускорением, которое будем обозначать также буквой а с верхним индексом k. Для определения ав можно написать два векторных уравнения: “в ~ °в х + а ЯВх + а ВВх + аХВВх ‘, ав =~ас + апв с + ахв с . Определяем величины и направления геометрических слагаемых в правых частях обоих уравнений: Ускорение Величина Направление “в х “в ‘1а в х = ( рЬх -Рц? ‘1 а в х , От точки Вх (фиг. 52, а) к точ­ке А, так как при вращении где pbx — длина вектора vB x на звена 1 с равномерной скоростью плане скоростей, приведенном полное ускорение равно нормаль­на фиг. 46, б, и pv — масштаб ному этого плана ^ВВ* v b b : Р == так к а к Р = 0 0 — au kr b 2ш ‘ VBBX = 2(0 (eex -[

xv ) , где Определяется вектором ско­eex — длина вектора на рости иВ в ^ повернутым на 90° плане скоростей в направлении вращения зве­на /, т. е. в данном случае по часовой стрелке. Скорость vbbx направлена вверх направо (см. вектор вх в на фиг. 46, б) парал­лельно звену /; следовательно, ускорение ав в направлено вправо перпендикулярно к зве­ну 1 аввх Неизвестна По звену 1 ас Равна нулю, так как точка С — неподвижна “вс v bc : 1вс — (с^-Ри)2 • h e , От точки В к точке С где cb — длина вектора vb q на — плане скоростей “вс Неизвестна Перпендикулярна к звену 3 Разделив величины ускорений на масштаб плана ускорений, определяем длины векторов. Приняв во внимание указанные выше направления всех векторов в

соответствии с первым из приведенных выше уравнений, проводим последова­тельно (фиг. 52, б) вектор -тс Ьх ускорения а в ^ вектор bx ksB x ускорения и линию действия ускорения ахв в . В соответствии со вторым уравнением от точки с, совпадающей с полюсом тс, проводим вектор cnB Q ускорения а ^ с и из конца этого вектора линию действия ускорения ав с . Точкой b пересечения линий действия уско­р е н и й ^ ^ и Ъв с определяется конец вектора тс b ускорения а^-Кинематические диаграммы 41 Пример 5. Построить план ускорений для шарнирного четырехзвенного меха­низма в положении, приведенном на фиг. 122,а, по данным, приведенным на стр. 108, и определить ускорения а ^ , а$2 и а$3 центров тяжести (числовой

пример). Пример 6. Построить план ускорений для кривошипно-шатунного механизма в положении, приведенном на фиг. 123,а, по данным, приведенным на стр. 112, и опре­делить ускорения a$v а$2 и ас (числовой пример). Пример 7. Построить план ускорений для шестизвенного механизма в поло­жении, приведенном на фиг. 124,а, по данным, приведенным на стр. 116, определить ускорения a$v а$2 , ас, а$^ и а$д и угловое ускорение звена EF.

Смотрите также:

Предмет Теория Машин и Механизмов ТММ

Определение положений механизма	Кинематические диаграммы
План скоростей	Аналитическое определение скоростей и ускорений