Оглавление:
Первый замечательный предел
При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел
называемый первым замечательным пределом. Читается: предел отношения синуса к его аргументу равен единице, когда
аргумент стремится к нулю. Докажем равенство (17.11).
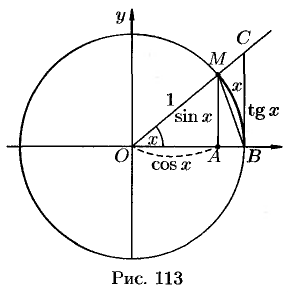
Возьмем круг радиуса 1, обозначим радианную меру угла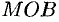 
через 
(см. рис. 113). Пусть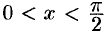 
. На рисунке 
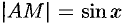, дуга 
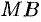численно равна центральному углу 
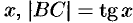. Очевидно, имеем 
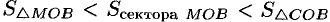. На основании соответствующих формул геометрии получаем 
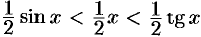. Разделим неравенства на 
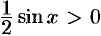, получим 
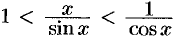или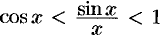 
.
Так как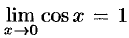 
и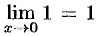 
, то по признаку (о пределе промежуточной функции) существования пределов
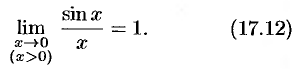
Пусть теперь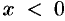 
. Имеем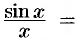 
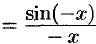, где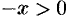 
. Поэтому
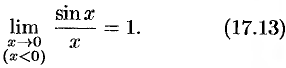
Из равенств (17.12) и (17.13) вытекает равенство (17.11).
Пример №17.6.
Найти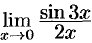 
.
Решение:
Имеем неопределенность вида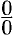 
. Теорема о пределе дроби неприменима. Обозначим 
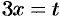; тогда пр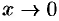и 
и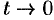 
, поэтому
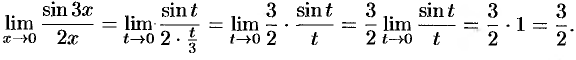
Дополнительный пример №17.7.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Сложная функция |
| Основные элементарные функции |
| Второй замечательный предел |
| Эквивалентные бесконечно малые функции |
