Оглавление:
Первый признак сравнения
Теорема. Если даны два ряда 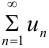 и
и 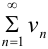 с неотрицательными членами, причём члены первого ряда не превосходят соответствующих членов второго ряда
с неотрицательными членами, причём члены первого ряда не превосходят соответствующих членов второго ряда 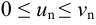 , то:
, то:
а) из сходимости второго (большего) ряда следует сходимость первого (меньшего) ряда;
б) из расходимости первого (меньшего) ряда следует расходимость второго (большего) ряда.
Задача №106.
Исследовать на сходимость ряд 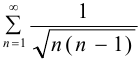 .
.
Решение:
Общий член данного ряда
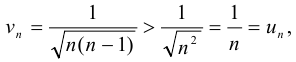
так как с увеличением знаменателя дробь уменьшается, а ряд 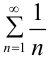 — гармонический, расходящийся. Следовательно, по признаку сравнения расходится и данный ряд.
— гармонический, расходящийся. Следовательно, по признаку сравнения расходится и данный ряд.
Задача №107.
Исследовать на сходимость ряд 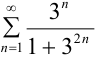 .
.
Решение:
Сравним данный ряд, общий член которого 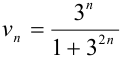 , с геометрическим рядом
, с геометрическим рядом
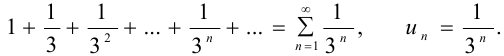
Так как 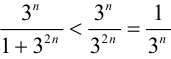 , т. е. выполнено условие
, т. е. выполнено условие 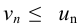 , а ряд
, а ряд 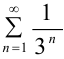 — сходится, значит по первому признаку сравнения сходится и данный ряд.
— сходится, значит по первому признаку сравнения сходится и данный ряд.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

